Question

X^2-9/(x+1)(x-3)> =0. (Меньше либо равно)
Объясните я не знаю у кого с Почему в этом примере X не может быть

Answer 1

$\dfrac{x^2-9}{(x+1)(x-3)}\geq 0\; \; ,\; \; \; ODZ:\; \left\{\begin{array}{ccc}x+1\neq 0\\x-3\ne 0\end{array}\right\; \left\{\begin{array}{ccc}x\ne -1\\x\ne 3\end{array}\right$

Выражение, стоящее в знаменателе, не может быть равно нулю, так как на 0 делить нельзя. В знаменателе записано произведение двух множителей. Поэтому каждый множитель не может равняться 0 .

Соответственно получим ОДЗ: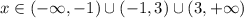   $x\in (-\infty ,-1)\cup (-1,3)\cup (3,+\infty )$  .

$\dfrac{(x-3)(x+3)}{(x+1)(x-3)}\geq 0\; \; \; \Rightarrow \qquad \; \; \dfrac{x+3}{x+1}\geq 0\; ,\; x\ne -1\; ,\; x\ne 3\\\\znaki:\; \; +++[-3\; ]---(\, -1\; )+++(\; 3\; )+++\\\\x\in (-\infty ;-3\; ]\cup (-1;3)\cup (3;+\infty )$

Answer 2

потому если подставить 3, то во второй скобке получится 0. а на ноль делить нельзя!