2. первый член 12, знаменатель 6/12=1/2,
Энный член геометрической прогрессии ищем по формуле bn=b₁*qⁿ⁻¹
b₇=b₁*q⁷⁻¹=b₁*q⁶;
b₇=12*(1/2)⁶=12/64=3/16;
2. b₈=b₁*q⁷=14;
b₁₀=b₁*q⁹=126; разделим b₁₀/b₈=q²=9; q=±3; b₁=14/(±3)⁷=±14/3⁷, используем характеристическое свойство геометрической прогрессии, найдем b₉²=b₈*b₁₀,
b₉²=b₈*b₁₀=126*14;
значит, b₉=±14*3=±42
S₇=b₁*(q⁷-1)/(q-1)
если q=3, S₇=(14/3⁷)*(3⁷-1)/(3-1)=14*2186*/(2*2187)=7*2186*/2187=15302/2187
6 2180/2187
если q=-3, то S₇=
(-14/3⁷)*((-3)⁷-1)/(-3-1)=-14*2188*/(4*2187)=-7*2188*/(2*2187)=-1094*7/2187=
-7658/2187=-3 1097/2187
4. 4.(5)=4+05555=4+0.5+0.05+0.005+...
q=0.05/0.5=0.1
s=0.5/(1-0.1)=5/9
4.(5)=4+(5/9)=4 5/9
Відповідь:
66 или 68
Пояснення:
Пусть х - число монет в первом столбике, тогда х+1 - во втором, х+3 - в третьем, х+n- в n-столбце
Имеем арифметическую прогрессию с начальним значением=х, d=1. n+1 елементов, тогда можем записать сумму
(2х+n)/2 ×(n+1)=2021
х=2021/(n+1) -n/2
2021=43×47 розложение на простие делители, поетому столбиков может бить 43 или 47
Значит n может равняться 42 или 46
При n=42 по формуле имеем х=26. поетому количество монет в последнем максимальном столбике = х+n=68
При n=46. х=20 тогда монет будет 66
Объяснение:
Домножим верхнее число на 2 и получим:
И просто все сложим и получим
14x=7⇒x=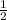
Теперь вместо x подставляем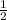
и получаем y.