Воспользуемся формулой 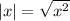 :
:
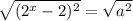
Возведем обе части в квадрат:
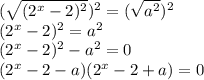
Рассмотрим 3 случая :
1.
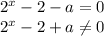
----------------------
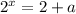
Мы знаем, что любое число(кроме 0) в любой степени больше нуля, то есть 2+а > 0 => a>-2
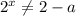
Так же 2-а уже должно быть меньше или равно нулю:
2-a ≤ 0 => a ≥ 2
Найдем пересечение => a ≥ 2
2.
По тому же принципу :
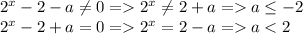
Найдем пересечение => a ≤-2
3.
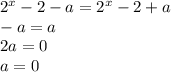
----------------------------------------------------------------------
Объединим три ответа => a Є (-∞ ; -2] U [2 ; +∞)
ответ : a Є (-∞ ; -2] U [2 ; +∞) U {0}
P.S это одно из возможных решений, возможно вы найдете и по проще)
ответ:х(х-у)^2
Объяснение: