Вход
Регистрация
Спроси Mozg AI
М
Молодежь
К
Компьютеры-и-электроника
Д
Дом-и-сад
С
Стиль-и-уход-за-собой
П
Праздники-и-традиции
Т
Транспорт
П
Путешествия
С
Семейная-жизнь
Ф
Философия-и-религия
Б
Без категории
М
Мир-работы
Х
Хобби-и-рукоделие
И
Искусство-и-развлечения
В
Взаимоотношения
З
Здоровье
К
Кулинария-и-гостеприимство
Ф
Финансы-и-бизнес
П
Питомцы-и-животные
О
Образование
О
Образование-и-коммуникации
.....больше.....
..меньше..
vlad20077
23.12.2020 12:35 •
Алгебра
Решите неполное квадратное уравнение:3х²+4х=0
👇
Увидеть ответ
Ответ:
настя7566
23.12.2020
0; -1
Объяснение:
x(3x + 4) = 0
x = 0
3x = -4
x = -1
4,6
(65 оценок)
Открыть все ответы
Ответ:
oksanka199800
23.12.2020
1)
a² + 5a + 6 = 0
D = 5² - 4 * 6 * 1 = 25 - 24 = 1
a₁ = (-5 + √1) / 2*1 = (-5 + 1) / 2 = -4 / 2 = -2
a₂ = (-5 - √1) / 2*1 = (-5 - 1) / 2 = -6 / 2 = -3
a² + 5a + 6 = (a + 2)(a + 3)
a² + 4a + 4 = 0
D = 4² - 4*4*1 = 16 - 16 = 0
a = -4 / 2*1 = -2
a² + 4a + 4 = (a + 2)(a + 2)
ответ: a+3 / a+2
2)
x² + 3x + 2 = 0
D = 9 - 8 = 1
x₁ = (-3+1) / 2 = -2 / 2 = -1
x₂ = -4 / 2 = -2
x² + 3x + 2 = (x + 1)(x + 2)
x² + 6x + 5 = 0
D = 36 - 20 = 16
x₁ = (-6 + 4) / 2 = -2 / 2 = -1
x₂ = -10 / 2 = -5
x² + 6x + 5 = (x + 1)(x + 5)
ответ: x+2 / x+5
3)
m² + 2m + 1 = 0
D = 4 - 4 = 0
m = -2/2 = -1
m² + 2m + 1 = (m + 1)(m + 1)
m² + 8m + 7 = 0
D = 64 - 28 = 36
m₁ = (-8+6) / 2 = -2 / 2 = -1
m₂ = (-8-6) / 2 = -14 / 2 = -7
ответ: m+1 / m+7
4,4
(17 оценок)
Ответ:
медведь44
23.12.2020
1. Условие неполное.
2.
Знаменатель геометрической прогрессии:
Вычислим теперь восьмой член геометрической прогрессии:
ответ:
3. Дано:
Найти:
Решение:
Вычислим знаменатель геометрической прогрессии:
Сумма
первых членов вычисляется по формуле:
Сумма первых
-ми членов геометрической прогрессии:
4.
Первый член геометрической прогрессии:
Cумма первых 5-ти членов геометрической прогрессии:
5.
Знаменатель:
Видим, что каждая последовательность умножается на 5. Следовательно, заданная последовательность - геометрическая прогрессия
4,5
(81 оценок)
Это интересно:
О
Образование
06.01.2021
Клюква стоит 250 рублей за кг, а малина 200....
О
Образование
16.03.2023
Решить систему уравнений x2 + y2 + xy = 3...
О
Образование
05.08.2020
Решить систему уравнений x2 + xy +y2 = 13...
О
Образование
06.04.2022
В треугольнике АВС проведена биссектриса АК...
О
Образование
11.03.2020
Водитель ехал с постоянной скоростью из города А в город Б...
О
Образование
27.04.2022
Первые 300 км автомобиль ехал со скоростью 60 км/час...
О
Образование
02.06.2023
В треугольнике АВС точка D на стороне АВ...
О
Образование
21.07.2020
Из разных городов, расстояние между которыми 600 км...
О
Образование
29.01.2020
Из пункта А в пункт B, расстояние между которыми 84 км...
Х
Хобби-и-рукоделие
21.02.2021
Правила и техника игры в карточную игру Скорость...
Новые ответы от MOGZ: Алгебра
Кирилл6901
20.12.2022
Найдите значения выражения 8a-11b при a= -7, = -3...
iambigboy
20.12.2022
Найдите координаты точек пересечения графика линейного уравнения -3x+2y-6=0 с осями координат....
tttyadoyan235
03.03.2023
Выбери многочлены, которые при разложении на множители содержат одинаковый множитель: 2x−4;2x−24m+1;−8−24m;21mn+7n;−5x+7n;x2−2x. Выбери правильные ответы: 2x−4;2x−24m+1 −8−24m;2x−24m+1...
evasyperandreev
16.05.2023
Упростите числовое выражение. Результат запишите в виде loga b. Найдите его приближенное значение с калькулятора....
UzZzeR
31.08.2021
Укажите наименьшее значение выражения |x+4|+|x+5|...
jessicagallagher
09.12.2021
Разложите на множители: x^9y^12+3x^2y^4z^4-3x^6y^8z^2-z^6 если не понятно, посмотрите на фото!Заранее поклон и благодарность!...
alekseqhhhh
25.01.2022
Найти значение выражения с решением(у-4)^2-у(у-5)-10 при у=1/3...
гсооагвгв
26.08.2020
В таблице представлена урожайность морковки в 2020 году Урожайностьц/га 1-5 5-10 10-15 15-20 Число хозяйств 10. 12 Накопленная частота. 18. 42 Памагите надо...
lizafedkovich
08.07.2020
Вычислить наиболее рациональным 18^2-15^2/33+18•15 ...
Topergggg
08.08.2020
.(Найдите координаты точек, в которых прямая mn, где m(2; 4) и n(5; -2),пересекает коордитаны оси.)....
MOGZ ответил
Путь от дома до магазина мальчик за 12мин, а от магазина до аптеки - за 18...
Вмагазин 120 телевизоров.шестую часть всех телевизоров продали в этот день,а...
Каковы носители зарядов в растворе поваренной соли...
Чем многоклеточные водоросли отличаются от одноклеточных водорослей...
Простое с обращением.2.простое с однородными членами и обобщающим словом....
Запиши выражение и найди его значение. 1) 8 уменьшить на 0 2) 3 увеличить...
Решить 2 по 10 класс №1 решите уравнение 4sin^2*(2x)+3sin2x-7=0 №2 найдите...
Вставь пропущенные буквы.поставь вопросы к глаголам.укажи время. ....
Раздели слово миллион на слог для переноса...
Название картин и их художников где есть изображение колоколов...
Полный доступ к MOGZ
Живи умнее Безлимитный доступ к MOGZ
Оформи подписку
О НАС
О нас
Блог
Условия пользования
Авторское право
Политика конфиденциальности
Предпочтения cookie-файлов
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
App
Вход
Регистрация
Что ты хочешь узнать?
Спроси Mozg
Открыть лучший ответ
0; -1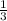
Объяснение:
x(3x + 4) = 0
x = 0
3x = -4
x = -1