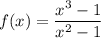
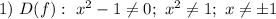
Следовательно, 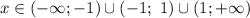
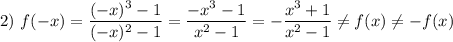 , значит, функция ни четная, ни нечетная; непериодическая.
, значит, функция ни четная, ни нечетная; непериодическая.
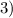 Если
Если 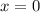 , то
, то 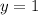 , значит (0; 1) — точка пересечения с осью ординат. Если
, значит (0; 1) — точка пересечения с осью ординат. Если 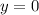 , то есть
, то есть 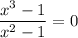 , то
, то 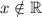 . Таким образом, функция не имеет точек пересечения с осью абсцисс.
. Таким образом, функция не имеет точек пересечения с осью абсцисс.
Значит, (0; 1) — единственная точка пересечения графика функции с осями координат.
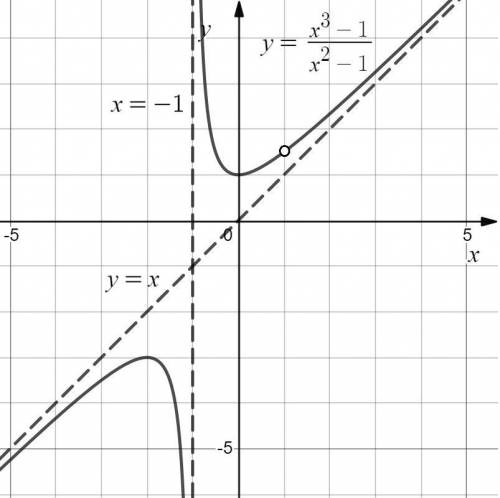
 Поскольку
Поскольку 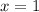 и
и 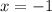 — точки разрыва функции и
— точки разрыва функции и 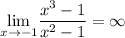 и
и 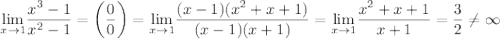 , то
, то 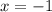 — вертикальная асимптота.
— вертикальная асимптота.
Если 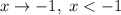 , то
, то 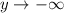 ; если
; если 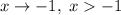 , то
, то 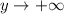 .
.
Найдем наклонные асимптоты 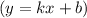 :
:
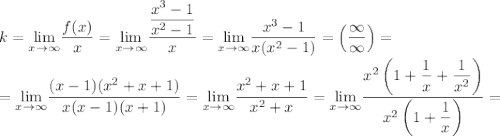
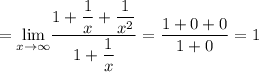
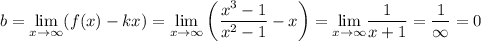
Следовательно, 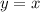 — наклонная асимптота.
— наклонная асимптота.
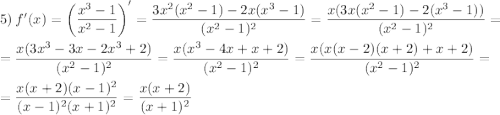
Найдем критические точки, приравняв первую производную к нулю: 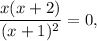 откуда
откуда 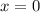 и
и  .
.
Заполним таблицу №1 (см. вложение).
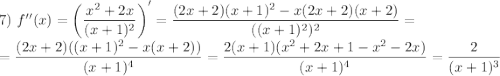
Если 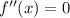 , то есть
, то есть 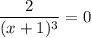 , то
, то 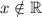 , значит, нет точек перегиба.
, значит, нет точек перегиба.
Систематизируем данные, полученные по второй производной, в таблицу №2.
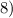 График функции изображен на рисунке (см. вложение).
График функции изображен на рисунке (см. вложение).
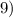 Из графика делаем вывод:
Из графика делаем вывод:
![E(f): \ y \in (-\infty; -3] \cup [1; +\infty)](/tpl/images/1059/8179/fda75.png)
ООФ: x ∈ (-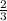 ;4)
;4)
Объяснение:
I. Найдем точки, в которых знаменатель дроби будет равен нулю:
1) 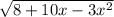 = 0 - корень может быть равен 0, только если подкоренное выражение равно 0
= 0 - корень может быть равен 0, только если подкоренное выражение равно 0
2) 8 + 10x - 3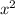 = 0
= 0
3) 3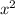 - 10x - 8 = 0
- 10x - 8 = 0
D = 100 + 96 = 196 = 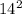
x₁ = 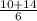 = 4
= 4
x₂ = 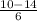 = -
= -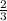
x ∈ (-∞; -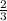 )∪(-
)∪(-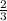 ;4)∪(4;∞)
;4)∪(4;∞)
II. Подкоренное выражение не может быть отрицательным, поэтому 8 + 10x - 3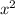 должно быть больше или равно нулю
должно быть больше или равно нулю
1) 8 + 10x - 3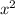 ≥ 0
≥ 0
Корни те же: x₁ = 4 и x₂ = -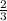
Так как нам нужны положительные значения, и у нас парабола ветвями вниз, то берем все точки между полученными корнями.
Выходит: x ∈ [-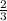 ; 4]
; 4]
III. Сводим эти значения в одну систему:
x ∈ (-∞; -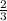 )∪(-
)∪(-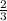 ;4)∪(4;∞)
;4)∪(4;∞)
x ∈ [-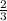 ; 4]
; 4]
Пересечение - x ∈ (-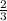 ;4)
;4)
1) х принадлежит (-∞;0) U (3;8)
2) х принадлежит (-∞;-6][8;+∞)