1.) Найти область определения
область определения это все "х" при котором уравнеие функции имееер решение.
например y=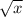
область определения будет все х>или=0 (т.к. корень из отрицательного числа нельзя вывести)
или например у=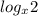
здесь обл. опр. х>0 и не равен нулю.
в твоем примере х Любой.
3) Выяснить наличие асимптот
асимптота- прямая к которой стремится график функции но никогда с ним не прикоснется. в твоем примере асимптоы нет. а например tgx имеет асимптоты в при тех х в которых tg не существует (-90, 90, 270...)
4) Найти точки пересечения графика с осями координат
здесь все просто: сначала приравниваем у к 0 и находим х. (это будут точки пересечения с осью х) на твоем примере 
x=+1;-1;
; 
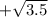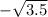значит точки (1;0) (-1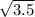;0) (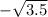
;0) (;0)
затем аналогично берем х за 0 и находим у. (это пересечение с осью у) точка(0;7)
вот и все!
1)разложим числитель и знаменатель на множители:(2x^2-x-1)^2=((х-1)(2х+1))^2 (x^3+2x^2-x-2)=(x-1)(x^2+3x+2) Подставим и сократим:Lim{x-1}(x-1)(2x+1)^2/(x^2+3x+2)=0 Получим сверху 0, а снижу число, т.е. =0 2)Вспомним формулы:1-cos 2x=2sin²x cos 7x- cos 5x=-2sin5xsin2x Тогда подставим в лимит: lim{x-0}2sin²x/-2sin5x*sin2x воспользуемся формулами эквивалентности: lim{x-0}2х²/-2*5x*2x=-0.1 3)Задание на 2ой замечательный предел.Формула имеет вид:lim(1+1/x)^x=е, приведем к такому виду наш предел: Lim((x-1)/(x+3))^(x+2)=lim((x-1)/(x+3)+1-1)^(x+2)=lim(1-4/x-5)^(x+2)*-4(x-5)/-4*(x-5)=lime^-4(x+2)/x-5=e^-4=1/e^4