В квадрат, сторона которого равна 36 см, вписан другой квадрат, вершины которого являются серединами сторон первого квадрата, в этот квадрат вписан таким же образом другой квадрат, и т. д. (см. рис.).
Найди сумму площадей всех квадратов.
Сумма площадей всех квадратов равна
см2
Дополнительные во сторона третьего по порядку квадрата равна
см.
2. Площадь наибольшего квадрата равна
см2.
3. Знаменатель равен
.
4. Выбери, какую из формул надо использовать в решении задачи:
b1(1−qn)1−q
b11−q2
(b1+b2)q2
b11−q
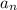=a₁+d(n-1)
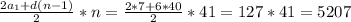n-1=240:6
(2^2)^log_2(x-4)<=36
2^{2*log_2(x-4)}<=36
2^log_2{(x-4)^2}<=36
По свойству получаем, что:
(x-4)^2<=36
(x-4)^2-36<=0
(x-4-6)*(x-4+6)<=0
(x-10)*(x+2)<=0
Решаем неравенство методом интервалов. Находим при каких икс левая часть рпвна нулю:
x-10=0 <=> x=10
x+2=0 <=> x=-2
На числовой оси иксов ставим точки -2 и 10. Знаки на получившихся интервалах: плюс, минус, плюс. Нам нужен минус, значит икс принадлежит отрезку [-2;10].
С учетом ОДЗ x c (4; 10].