Объяснение:
Решение задачи:
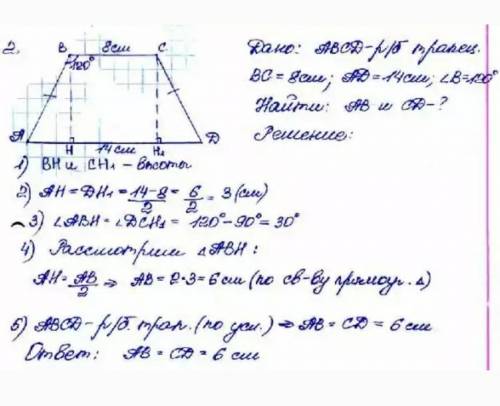
Рассмотрим равнобедренную трапецию АВСД. С углов В и с опустим перпендикуляры ВК и СМ на основание АД. Образовался прямоугольник КВСМ и два прямоугольных треугольника АВК и МСД. Рассмотрим треугольник АВК. Угол АКВ прямой и равен 90 градусов. Угол АВК равен 120 - 90 = 30 градусов. Сторона Ак равна (14 - 8) / 2 = 3 сантиметра. Катет прямоугольного треугольника АВК лежит против угла в 30 градусов, а значит гипотенуза АВ равна 2 * 3 = 6 сантиметров.
ответ: Боковые стороны трапеции равны 6 сантиметров.


 или х₂ = 1
или х₂ = 1
выразим у через х, у=(-5х+8) : 2= -2,5х+4
Зх+2,5х-4=7
5,5х=11
х=2
у=-2,5Х+4=-2,5*2+4=-1