ответ: 1-й рабочий сделает всю работу за 18 часов, а 2-й - за 24 часа.
Пусть время 1-го рабочего, затраченное на всю работу - х, а 2-го рабочего - у.
Тогда производительность 1-го рабочего 1/х, а 2-го рабочего - 1/у.
7/х -работа 1-го рабочего в течение 7 часов, 4/у - работа 2-го рабочего в течение 4-х часов. Они выполнили 5/9 всей работы.
7/х + 4/у = 5/9 (1)
осталось им выполнить 4/9 работы.
Работа 1-го рабочего за 4 часа 4/х, 2-го рабочего за 4 часа - 4/у.
После этого осталось 1/18 работы.
4/9 - (4/х + 4/у) = 1/18 (2)
Из (1) 4/у = 5/9 - 7/х (3)
Подставим (3) в (2)
4/9 - (4/х + 5/9 - 7/х ) = 1/18
4/9 - 4/х - 5/9 + 7/х = 1/18
- 1/9 + 3/х = 1/18
3/х = 3/18
х = 18
из (3) 4/у = 5/9 - 7/18
4/у = 10/18 - 7/18
4/у = 1/6
у = 24
Объяснение:
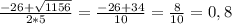

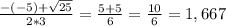

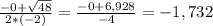
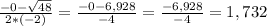
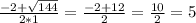
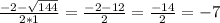
x−1x−x+15=x2−12
\frac{x(x+1)-5(x-1)}{x^{2}-1} = \frac{2}{ x^{2} -1}x2−1x(x+1)−5(x−1)=x2−12
Найдем область допустимых значений: x^{2}-1x2−1 = x^{2}-2x-1x2−2x−1
Далее по Виета
\left \{ {{x_{1}x_{2} =1} \atop {x_{1}+x_{2} =2}} \right.{x1+x2=2x1x2=1
получаем x_{1} =1x1=1 x_{2} =2x2=2
эти корни недоступны...
Умножаем обе части на x^{2}-1x2−1
x(x+1)-5(x-1)=2
x^{2}-4x+5=2x2−4x+5=2
x^{2}-4x+3=0x2−4x+3=0
Далее по Виета \left \{ {{x_{1}x_{2} =3} \atop {x_{1}+x_{2} =4}} \right.{x1+x2=4x1x2=3
получаем x_{1} =1x1=1 x_{2} =3x2=3
только x_{1} =1x1=1 не может быть решением потому что недоступно