По формуле:
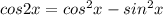
Зная это получаем:
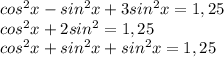
Известно что:
отсюда получаем:
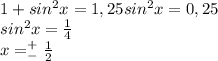
Получаем 2 уравнения:
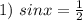это табличное значение синуса и получается 2 решения:
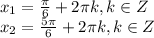
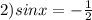аналогично получаем 2 решения:
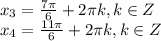
Теперь обратим внимание, что эти 4 решения можно записать в 2 решения в виде:
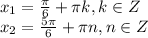
Теперь надо найти при каких значениях k и n решения лежат на отрезке ![[0; \frac{5\pi}{2}]](/tpl/images/0071/0603/9e0ce.png)
Для этого решаем 2 неравенства
1) 
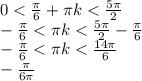
Так как к у нас принадлежит целым числам, то получается что к=0,1,2
2) Теперь ищем n, аналогично:
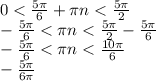
Поскольку n принадлежит целым числам, то получается что n=0,1
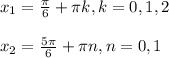
D=64-12=52 x²=1/2[8-√52] x²=1/2[8+√52]
функция четная достаточно построить при х>0 и отразить симметрично относительно оси у.
y'=4x³-16x=4x(x²-4)=4x(x+2)(x-2)
-202
- + - + "+" возрастает "-" убывает
график при x≥0
линия выходит из х=0 у=3 идет вниз пересекает ось х при х≈0,6 продолжает снижаться до минимума при х=2 достигая значения
у(2)=-13 затем возрастает и пересекает ось х при х≈2,7 и растет до
+∞
для х отрицательных отразить зеркально оси у.