см, тогда второй катет - 
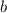см. Площадь прямоугольного треугольника равна 
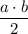, что составляет 210 см² или перепишем сразу 
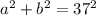
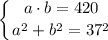
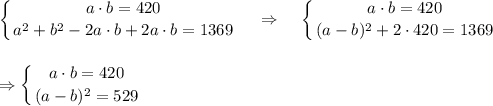
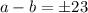. Тогда имеем несколько случаев.
, то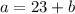 
и подставим в первое уравнение.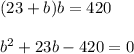
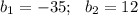см и корень 
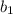не удовлетворяет заданному условию
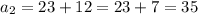см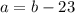
,то подставив в первое уравнение, получим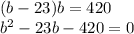
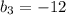
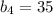см и корень 
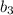не удовлетворяет условию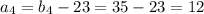
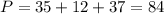см
(Доказательство иррациональности числа sqrt(2): пусть sqrt(2) = m/n, m/n - несократимая дробь, m,n — натуральные числа. Возводим в квадрат, домножаем на n^2, получаем m^2 = 2n^2, откуда m — чётное. Пусть m = 2M. Подставляем, сокращаем на 2, получаем n^2 = 2M^2, откуда n — тоже чётное, что противоречит предположению о несократимости дроби m/n)
2) Пусть число sqrt(5) + sqrt(2) - 1 рациональное, тогда и sqrt(5) + sqrt(2) тоже рациональное, и (sqrt(5) + sqrt(2))^2 = 5 + 2 + 2sqrt(10) = 7 + 2 sqrt(10) рациональное, тогда и sqrt(10) тоже рациональное. Но sqrt(10) — иррациональное, противоречие. Значит, sqrt(5) + sqrt(2) - 1 — иррациональное.
Иррациональность sqrt(10) доказывается аналогично: sqrt(10) = m/n, m^2 = 10n^2. Дальше можно, наример, точно так же, как и в примере выше, доказать, что m и n должны быть чётными.