М 19
Объяснение:
Шаровое скопление M 19 (также известное как M 19 или NGC 6273) является шаровым звёздным скоплением в созвездии Змееносца.
Шаровое скопление M 19
Шаровое скопление
Messier object 019.jpg
История исследования
Открыватель
Шарль Мессье
Дата открытия
1764
Наблюдательные данные
(Эпоха J2000.0)
Прямое восхождение
17ч 02м 37с
Склонение
-26° 16′ 04″
Расстояние
28 000 св. лет (8600 пк)
Видимая звёздная величина (V)
6,8
Видимые размеры (V)
17,0′
Созвездие
Змееносец
Физические характеристики
Класс
VIII
Часть от
Млечный Путь
Радиус
70 св.лет
Абсолютная звёздная величина (V)
−9,13[1]
Возраст
70 св. лет
Информация в базах данных
SIMBAD
M 19э
1.
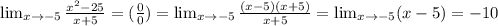
2.
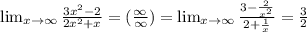
3. нет. Но не понял задания: нужно графически или аналитически определить? в любом случае график функции думаю вы сами сможете нарисовать.
4
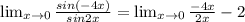
5
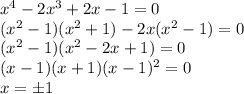
Объяснение:
Если не возникает неопределенностей (посмотрите, например, в и-нете "неопределенности пределов"), то для вычисления предела достаточно подставить вместо x, то к чему он стремится. Иначе, если появляются неопределенности, нужно их раскрыть(в этом все решение пределов). Есть множество методов решения различных неопределенностей (разложение на множители, деление числителя и знаметеля на высшую степень(только при x->∞), и т.д.).
для решения задания 4 был использован первый замечательный предел:
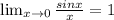
То есть в некоторых случаях можно сказать, что sinx ~ x, при x->0.
че ты врешь ты даешь 10 балов а 100
Объяснение: