Двухзначное число больше удвоенного произведения его цифр на 5, а от удвоенной суммы цифр - на 3. Найдите эти число.
Решение.
Пусть x - цифра десятков данного числа;
y - цифра единиц этого числа
тогда
(10x+у) - данное двухзначное число.
ОДЗ: х∈N; 1≤x≤9;
y∈N; 0≤y≤9
По условию 10х+у > 2·(x·y) на 5.
Получаем первое уравнение:
10x+у - 2xy = 5
И ещё по условию 10х+у > 2·(x+y) на 3.
Получаем второе уравнение:
10x+у - 2·(x+y) = 3
Упростим его:
10x+у-2x-2y = 3
8х - у = 3
Решаем систему:
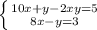
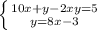
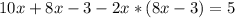
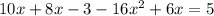
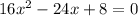
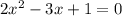
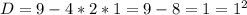
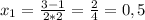 ∉N
∉N
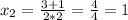
y=8x-3 при x=1
y=8·1-3
y=5
1- цифра десятков данного числа;
5 - цифра единиц этого числа
ответ: 15.
1. 4x-3=3x+7
x=10
2. угол А + угол В + угол С= 180 градусам
Пусть угол(А)=a, угол(В)=b, угол(С)=c
a+b+c=180
a=3b
c=2a=6b
3b+b+6b=180
b=18
a=54
c=108
3. a) x-y=1
x+y=3
складываем и получаем 2x=4
x=2 и y=1
б) 2x-3y=3
3x + 2y= 33
умножаем 1-ое уравнение на 2 и 2-ое на 3
складываем и получаем 13x=39
x=3 и y=1
4. x+y=210
x/2 + 2y = 240
умножаем 2-ое уравнение на 2 и получаем
x+4y=480
вычитаем из 2-го уравнения 1-ое и получаем
3x=270
x=90 и y=120
2/(x+1)+2/(x-1)=11/30
*домножаем на нижние части всех дробей*
2*30(x-1)+2*30(x+1)=11(x-1)(x+1)
60x-60+60x+60=11x^2-11
-11x^2+120x+11=0
*умножаем на (-1)*
11x^2-120x-11=0
a=11; b= -120; c= - 11
D=b^2-4ac
D=144884>0, значит 2 действительных корня.
X1=(120+122)/22=11
X2=(120-122)/11= - 1/11
ответ : 11; - 1/11