Если цифра 5 стоит первая, а за ней другие три цифры. То на каждом по 9 вариантов. Решение:
Если цифра 5 не первая, а вторая, третья или четвертая, соответственно на первом месте может стоять любая цифра кроме 5 и 0. Значит это цифры 1 2 3 4 6 7 8 9 ⇒ Вариантов всего восемь. Остальные два числа имеют по девять вариантов. Решение:
Это у=синх, а синх+2, будет тоже самое, только график переместится по оси у не 2 единицы вверх. свойства Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок [1; 3], т. е. синус функция — ограниченная.
Функция нечетная: sin(−x)=−sin x для всех х ∈ R. График функции симметричен относительно точко (0,2).
Функция периодическая с наименьшим положительным периодом 2π:
sin(x+2π·k) +2 = sin x + 2, где k ∈ Z для всех х ∈ R. sin x +2 не равна 0 при x любое
sin x+2 > 0 (положительная) для всех x любое sin x +2< 0 (отрицательная) не бывает отрицательной.
Функция возрастает от 1 до 3 на промежутках: Функция убывает от 1 до 3 на промежутках: Наибольшее значение функции sin x+2 = 3 в точках: х= пи/2+2π·k где k ∈ Z Наименьшее значение функции sin x +2 = 1 в точках: х=3пи/2+2π·k где k ∈ Z
Дана функция y=f(x) где f(x) = { -x +1, если -4 < x < -1 -x² + 3, если -1 < x < 2 а) f(-4)= -(-4) +1=5 f(-1)= -(-1) +1=2 f(0)= -(0)^2 +3=3
б) график функции в дополнении
в) функция определена на ограниченном интервале функция на данном интервале непрерывна, функция на данном интервале не является ни четной, ни нечетной функция на данном интервале не является монотонной, так как производная меняет знак производная имеет разрыв функция на данном интервале имеет 2 локальных максимума и 2 локальных минимума
Если цифра 5 стоит первая, а за ней другие три цифры. То на каждом по 9 вариантов. Решение: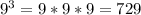
Если цифра 5 не первая, а вторая, третья или четвертая, соответственно на первом месте может стоять любая цифра кроме 5 и 0. Значит это цифры 1 2 3 4 6 7 8 9 ⇒ Вариантов всего восемь. Остальные два числа имеют по девять вариантов. Решение: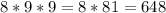
ответ: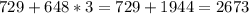 числа.
числа.