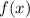необходимо найти ноли производной 
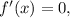т.е. точки, где у функции будет экстремум, и показать, что до экстремума функция 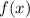падает, т.е. производная 
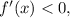а после экстремума функция растёт, т.е. производная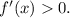 
;
;
;
;
;
;
;
;
;
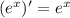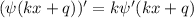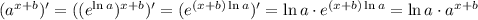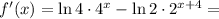
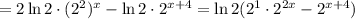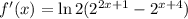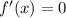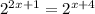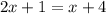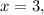причём это единственный корень.
например при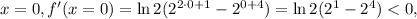 
т.е. функция убывает.
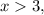например при 
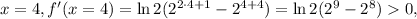т.е. функция растёт.
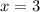как раз достигается минимум: 
;
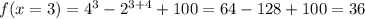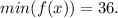
В таблицах значений х и у.
Объяснение:
Построить в разных системах координат графики функций.
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
y= -x-2 y=x+2
Таблицы:
х -1 0 1 х -1 0 1
у -1 -2 -3 у 1 2 3
y= -2x+3 y=x-4
х -1 0 1 х -1 0 1
у 5 3 1 у -5 -4 -3