Question

2x^2+4x^2-7x+1> =0 пришёл к такому выполняя 15 пробник, дорешить

Answer 1

$2x^2+4x^2-7x+1\geq 0\; \; \Rightarrow \; \; \; 6x^2-7x+1\geq 0$

Здесь легко подобрать один корень квадратного трёхчлена:

х=1, так как 6*1-7*1+1=0 . А второй корень по теореме Виета:

$x_1\cdot x_2=1\cdot x_2=\frac{1}{6}\; \; \Rightarrow \; \; \; x_2=\frac{1}{6}\\\\6\, (x-1)(x-\frac{1}{6})\geq 0\\\\znaki:\; \; \; +++[\, \frac{1}{6}\, ]---[\, 1\, ]+++\\\\x\in (-\infty ,\frac{1}{6}\, ]\cup [\, 1,+\infty \, )$

Если же  условие было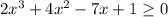  $2x^3+4x^2-7x+1\geq 0$  , то один корень тоже подбираем аналогично (действительный корень - делитель свободного члена). Корнем будет х=1. Затем делим заданный многочлен нацело на (х-1), получим (2х²+6х-1), корни которого легко найти .

$2x^3+4x^2-7x+1=(x-1)(2x^2+6x-1)\\\\2x^2+6x-1=0\; ,\; \; D/4=3^2-2\cdot (-1)=9+2=11\\\\x_{1}=\frac{-3-\sqrt{11}}{2}\approx -3,16\; \; ,\; \; x_2=\frac{-3+\sqrt{11}}{2}\approx 0,16\\\\2x^3+4x^2-7x+1=2\, (x-1)(x-\frac{-3-\sqrt{11}}{2})(x-\frac{-3+\sqrt{11}}{2})\geq 0\\\\znaki:\; \; ---[-3,16]+++[0,16\, ]---[\, 1\, ]+++\\\\x\in [\frac{-3-\sqrt{11}}{2},\frac{-3+\sqrt{11}}{2}\, ]\cup [\, 1,+\infty \, )$