Данное уравнение не имеет целых корней.
Используем метод Феррари:
уравнение вида
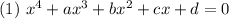
с замены 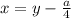
приводим к виду:
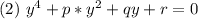
где:
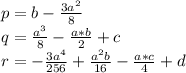
добавим и вычтем из левой части уравнения 2 выражение 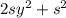 , где s - некоторое число:
, где s - некоторое число:

получим:
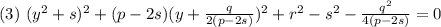
Пусть s - корень уравнения
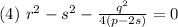
Тогда уравнение 3 примет вид:
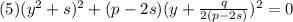
Избавляемся в уравнении 4 от знаменателя:
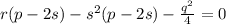
Раскроем скобки и получим:
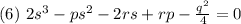
Уравнение 6 называется кубической резольвентой уравнения 4 степени.
Разложим уравнение 5 на множители:
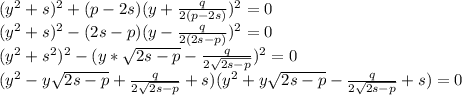
Получим два квадратных уравнения:
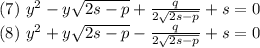
Применяем этот метод для решения уравнения
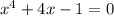
Перепишем уравнение в полном виде:
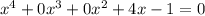
коэффиценты:
a=0
b=0
c=4
d=-1
определяем p,q и r:
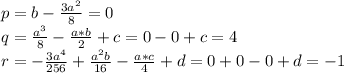
ищем s:
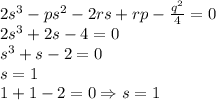
подставляем p,q,r и s в квадратные уравнения 7 и 8:
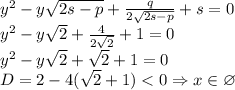
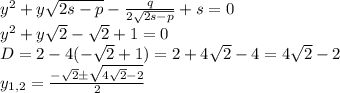
Теперь находим x:
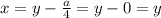
ответ: 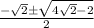
Согласно теореме Виета, сумма корней квадратного уравнения равна отрицательному коэффициенту b:
x1 + x2 = -b
Произведение корней квадратного уравнения в этой же теореме равно свободному коэффициенту с:
х1 × х2 = с
Доказательство:
Возьмём следующее уравнение:
х² + 6х - 7 = 0
Сначала решим его через дискриминант:
D = b² - 4ac = 36-4×(-7) = 36+28 = 64
x1,2 = (-b±√D)÷2a = (-6±8)÷2
x1 = (-6+8)÷2 = 1
x2 = (-6-8)÷2 = -7
Теперь решим это же уравнение через теорему Виета:
Мы знаем, что:
х1 + х2 = -b
x1 × x2 = c
Осталось лишь подобрать такие корни уравнения, которые бы подходили под эти два равенства. Путём нехитрых вычислений, находим, что этими корнями являются числа -7 и 1:
-7 + 1 = -6 = -b
-7×1 = -7 = c
ответы сходятся, значит наши рассуждения верны.
Это работает со всеми квадратными уравнениями, в которых коэффициент а = 1.
Теорема доказана.