х₁ = πn; x₂ = π/6 + 2πk; x₃ = 5π/6 + 2πm; n, k, m ∈ Z
Корни - 19π/6; -3π; -2π;
Объяснение:
sinx + 2sin(2x + π/6) = √3sin2x + 1
sinx + 2(sin2x · cos π/6 + cos2x · sin π/6) = √3sin2x + 1
sinx + 2(sin2x · 0.5√3 + cos2x ·0.5) = √3sin2x + 1
sinx + √3sin2x + cos2x = √3sin2x + 1
sinx + cos2x = 1
sinx + 1 - 2sin²x = 1
2sin²x - sinx = 0
sinx (2sinx - 1) = 0
1) sin x = 0
x = πn
б) корни на интервале [-7π/2; -2π]
--7π/2 ≤ πn ≤ -2π
-3.5 ≤ n ≤ -2
n = -3 и n = -2
корни -3π и -2π
2) 2sinx - 1 = 0
sinx = 1/2
x₂ = π/6 + 2πk
x₃ = 5π/6 + 2πm
б) корни на интервале [-7π/2; -2π]
-7π/2 ≤ π/6 + 2πk ≤ -2π
-7/2 - 1/6 ≤ 2k ≤ -2 - 1/6
-22/6 ≤ 2k ≤ -13/6
-11/6 ≤ k ≤ -13/12
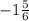 ≤ k ≤
≤ k ≤ 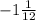
Корней нет
-7π/2 ≤ 5π/6 + 2πm ≤ -2π
-7/2 - 5/6 ≤ 2m ≤ -2 - 5/6
-26/6 ≤ 2m ≤ -17/6
-13/6 ≤ m ≤ -17/12
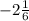 ≤ m ≤
≤ m ≤ 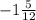
m = -2
Корень
5π/6 - 4π = - 19π/6
Разделить обе стороны уравнения на -2:
sin (x)=
Поскольку sin (t)=sin(π-t),уравнение имеет 2 решения:
sin (x)=
sin (π-x)=
Чтобы изолировать x/π-x,нужно использовать обратную тригонометрическую функцию:
x=arcsin (
x=arcsin (
Используя таблицу значений тригонометрических функций или единичную окружность,найдём значение arcsin(
x=
π-x=
Поскольку sin (x/π-x) является периодической функцией,нужно добавить период 2kπ,k∈Z для нахождения всех решений:
x=
π-x=
Решить уравнение относительно x:
x=
x=
Т.к. k∈Z,то -2kπ=2kπ:
x=
x=
Окончательное решение:
x=
2.cos (2x)-sin (x)=0
Используя cos (2t)=1-2sin (t²),записать выражение в развёрнутом виде:
1-2sin (x)²-sin (x)=0;
Решить уравнение используя подстановку t=sin (x):
1-2t²-t=0;
Решить уравнение относительно t:
t=
t=-1;
Сделать обратную подстановку t=sin (x):
sin (x)=
sin (x)=-1;
Решить уравнение относительно x:
x=
x=
x=
Найти объединение:
x=