В решении.
Объяснение:
В 12:00 Незнайка вышел из пункта А в пункт Б, расположенный в 8 км от пункта А, со скоростью 4 км/ч. Через час Чебурашка вышел навстречу Незнайке с той же скоростью из пункта Б. Встретившись, они остановились, сели на лавочку, поговорили 30 минут и отправились вместе в пункт Б со скоростью 2 км/ч.
а) Когда они оказались в пункте Б?
Незнайка и Чебурашка оказались в пункте Б в 15.00
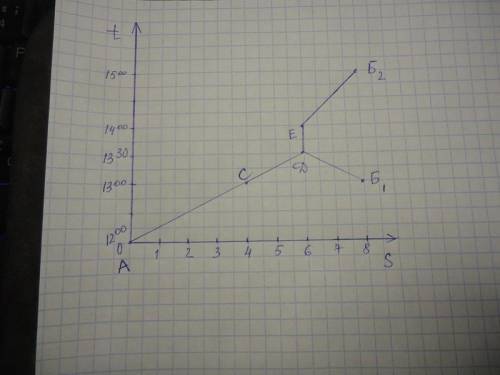
б) Постройте график движения обоих героев с 12:00 до момента их прибытия в пункт Б.
Пояснения к графику:
В момент выхода Чебурашки из пункта Б (точка на графике Б₁) Незнайка был в пути 1 час и км, точка на графике С, время 13.00.
В 13.00 Незнайка и Чебурашка начали движение навстречу друг другу с общей скоростью (скоростью сближения) 4+4=8 км/час, пройти им нужно было общее расстояние 4 км, и времени у них ушло 4 : 8 = 0,5 (часа). На графике место встречи точка Д, время 13.30.
Потом они посидели на лавочке 30 минут (0,5 часа), точка Е, время 14.00.
От точки Е начали движение в сторону пункта Б (на графике точка Б₂).
При скорости 2 км/час и расстоянии 2 км потратили на дорогу 1 час и оказались в пункте Б (точка Б₂) в 15.00.
в) Какой масштаб, на ваш взгляд, удобно выбрать по оси времени? а по оси расстояния?
По оси времени удобнее применить масштаб в 1 часе 2 см;
по оси расстояния в 1 см 1 км.
Найдем решения неравенства Ix-5I≤2; -2≤х-6≤2; 4≤х≤8- отрезок длиной 4
Найдем решения неравенства Ix-6I≥1
x-6≥1; х≥7 или х-6≤-1; х≤5; т.е. х∈(-∞;5]∪[7;8]
Из отрезка [4;8] выпадает только отрезок[5;7] длины 2
Используя геометрическое определение вероятности, найдем искомую вероятность, длина решений второго неравенства, которое находится в первом, составляет 2, это сумма длин отрезков [4;5] и [7;8], т.е. число благоприятствующих исходов равно 2, а общее число исходов 4, значит, вероятность равна 2/4=0.5
3a²+7a-6=0
D=49+72=121
a1=(-7-11)/6=-3⇒(2/3)^x=-3 нет решения
a2=(-7+11)/6=2/3⇒(2/3)^x=2/3⇒x=1