1. Решим первое неравенство этой системы:
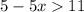
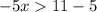
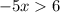
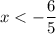
ответ: 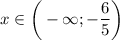
2. Дробь 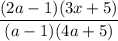 существует, если
существует, если
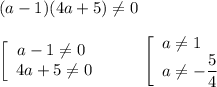
Перед тем как выражать  , нужно рассмотреть случаи, когда дробь
, нужно рассмотреть случаи, когда дробь 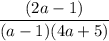 положительная, а когда отрицательная:
положительная, а когда отрицательная:
 знак неравенства меняться не будет (так как делим (умножаем) на положительное число):
знак неравенства меняться не будет (так как делим (умножаем) на положительное число):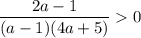
Решим неравенство методом интервалов.
а) ОДЗ: 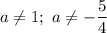
б) Нуль неравенства: 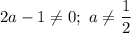
в) Решением данного неравенства будет 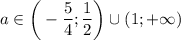 .
.
При таких значениях параметра  знак неравенства меняться не будет:
знак неравенства меняться не будет:
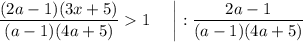
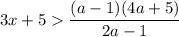
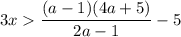
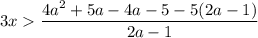
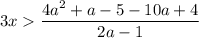
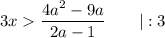
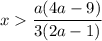
 знак неравенства измениться на противоположный (так как делим (умножаем) на отрицательное число):
знак неравенства измениться на противоположный (так как делим (умножаем) на отрицательное число):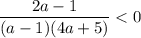
Решим неравенство методом интервалов. Решением данного неравенства будет  .
.
При таких значениях параметра  знак неравенства изменится:
знак неравенства изменится:
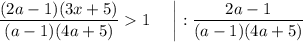
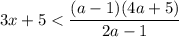
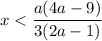
ответ: если  , то
, то 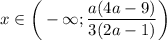 ; если
; если 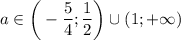 , то
, то 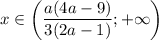 ; если
; если 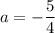 и
и 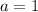 , то неравенство не имеет решений.
, то неравенство не имеет решений.
3. Данная система неравенств решается в зависимости от значений параметра  , поэтому:
, поэтому:
1) Рассмотрим случай, когда решение неравенств пересекается:
Если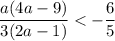 , то есть
, то есть 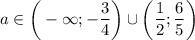 , то в объединении с
, то в объединении с 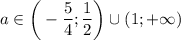 получаем
получаем 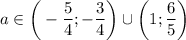
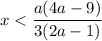 при
при  Если
Если 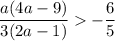 , то есть
, то есть 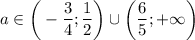 , то в объединении с
, то в объединении с  получаем, что таких
получаем, что таких  не существует, то есть такого варианта эта система не имеет.
не существует, то есть такого варианта эта система не имеет.2) Рассмотрим случай, когда решение неравенств не пересекается (когда система не имеет решений):
Оставшийся промежуток является решением этого варианта:![a \in \bigg[-\dfrac{3}{4}; \dfrac{1}{2} \bigg]\cup \bigg[\dfrac{6}{5}; + \infty \bigg) \cup \begin{Bmatrix} -\dfrac{5}{4}; 1 \end{Bmatrix}](/tpl/images/0595/8885/89750.png)
ответ: если  , то
, то 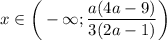 ; если
; если 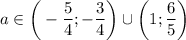 , то
, то 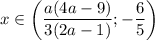 ; если
; если ![a \in \bigg[-\dfrac{3}{4}; \dfrac{1}{2} \bigg]\cup \bigg[\dfrac{6}{5}; + \infty \bigg) \cup \begin{Bmatrix} -\dfrac{5}{4}; 1 \end{Bmatrix}](/tpl/images/0595/8885/89750.png) , то система не имеет решений.
, то система не имеет решений.
2) Десятичные приближения по недостатку и по избытку - это десятичные дроби, между которыми заключено иррациональное число. Возьмём, например, √3~1,732. Его приближением до сотых долей по недостатку будет 1,73, а по избытку 1,74.
3) Классическое доказательство. Если √2 рационально, то его можно выразить несократимой дробью √2=a/b. Возведем все в квадрат. 2=a^2/b^2. То есть 2b^2=a^2. Теперь рассуждаем. Слева чётное число, значит a тоже чётное. Но чётный квадрат всегда делится на 4. Значит, b^2 тоже чётный. Но тогда а и b оба четные и дробь a/b можно сократить. Но мы условились, что дробь несократима. Противоречие. Значит, число √2 нельзя выразить дробью, то есть оно иррациональное.
4) Действительные - это все числа, и рациональные и иррациональные.
5) Действительные числа можно представить в виде точек на координатной прямой, причём это все точки на прямой.
6) Натуральные N, целые Z, рациональные Q, действительные R. Круги Эйлера нарисовать не могу, но могу объяснить. Действительные - самый большой круг, рациональные внутри, целые внутри рац-ных, натуральные внутри целых.