По условию скорость мотоциклиста больше скорости велосипедиста, значит,
10 км - это расстояние, которое проехал велосипедист до встречи;
тогда
50-10=40 км - это расстояние, которое проехал мотоциклист до встречи.
Пусть х км/ч - скорость велосипедиста, тогда
(х+30) км/ч - скорость мотоциклиста;
10/х ч - время движения велосипедиста до встречи;
40/(х+30) ч - время движения мотоциклиста до встречи.
По условию на движение до встречи каждый из них потратил одинаковое количество времени, получаем уравнение:

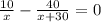
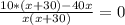
ОДЗ: x>0
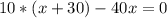



10 км/ч - скорость велосипедиста,
Из города А в город В выехали одновременно навстречу друг другу два автобуса. Расстояние между городами 180 км. Известно, что автобусы встретились через 2 часа. С какой скоростью двигался первый автобус, если ему потребовалось на прохождение всего пути на 54 минуты меньше, чем второму автобусу? ответ дайте в км/ч.
ответ: 50 км/ч.
Объяснение: 54 мин = 54/60 ч = 9/10 ч
Пусть скорость первого автобуса x км/ч , второго_км/ч
Можем составить систему уравнений :
{ 2x+2y =180 ; { 2(x +y)=2*90 ; {y =90 - x ;
{180/y - 180 /x =9/10. {9 *20(1/y-1/x ) = 9/10 {200(1/y -1/x) = 1 .
- - - - - - -
200( 1/(90 -x)- 1 /x ) = 1 ⇔ 200( x -90+x)/ =x(90 -x) ⇔
200(2x -90) =x(90 - x) ⇔ 400x -18000 = 90x -x²⇔
x² +310x -18000 =0 D =310² +4*1800 =96100 +72000=168100=410²
x₁ , ₂ = (-310±410) /2
x₁ = 50 ( км/ч ) , x₂= -360 < 0 _посторонний корень
Решение системы уравнений (21/32 (≈0,66); 7/8 (≈0,88)
Объяснение:
Решить систему уравнений:
5y+4x=7
4x−3y=0 методом сложения.
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.
В данной системе нужно любое из уравнений умножить на -1:
-4х-5у= -7
4x−3y=0
Складываем уравнения:
-4х+4х-5у-3у= -7
-8у= -7
у= -7/-8
у=7/8
Теперь подставляем значение у в любое из двух уравнений системы и вычисляем х:
5y+4x=7
4х=7-5у
4х=7-5*7/8
4х=21/8
х=21/8:4
х=21/32
Решение системы уравнений (21/32; 7/8)