З натуральних чисел від 1 до 171 складені всі можливі пари з різними елементами. Знайдіть серед них кількість пар добуток елементів яких ділиться на три

👇

Открыть все ответы

Ответ:

vaniev2006

16.12.2022

A =9x =4y +2 ;
Число a должна иметь вид : a =36k +18 .

Т.к. число a трехзначное, то 100<36k+18 <1000 ⇔3 ≤ k  ≤ 27.
Количество таких чисел:  n=27-(3-1) = 25 .
a∈{ 126 ; 162 , 198 ; ...972} * * * Составляют арифметическую прогрессию * * *
* !  702 = 126 +(n-1)36⇒n=17 * * *
702 =36k+18 при k =19.

* * * P.S. * * *
a = 9x = 4y +2 ; || 100 <9x <1000⇔12 <x ≤111 ||
y =(9x -2)/4 ;
y = 2x + (x-2)/4 ; k= (x-2)/4⇒x=4k+2 . || y =2x+k =2(4k+2)+k =9k+4 ||
⇒ { x =4k +2 . y =9k+4 .
|| 12 ≤ 4k+2 ≤ 111⇔2,5  ≤ k ≤27,25 ; 3 ≤ k ≤ 27 ||
a =9x =36k+18.

число  a =9x =9(4k +2) =36k +18.

4,8(1 оценок)

Ответ:

bekbolata45

16.12.2022

1-ое уравнение:

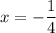
$x=-\dfrac{1}{4}$

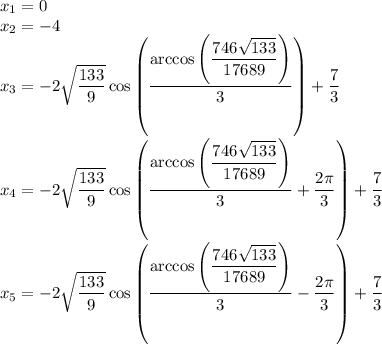
2-ое уравнение:

$x_1=0\\x_2=-4\\x_3=-2\sqrt{\dfrac{133}{9}}\cos\left(\dfrac{\arccos\left(\dfrac{746\sqrt{133}}{17689}\right)}{3}\right)+\dfrac{7}{3}\\x_4=-2\sqrt{\dfrac{133}{9}}\cos\left(\dfrac{\arccos\left(\dfrac{746\sqrt{133}}{17689}\right)}{3}+\dfrac{2\pi}{3}\right)+\dfrac{7}{3}\\x_5=-2\sqrt{\dfrac{133}{9}}\cos\left(\dfrac{\arccos\left(\dfrac{746\sqrt{133}}{17689}\right)}{3}-\dfrac{2\pi}{3}\right)+\dfrac{7}{3}\\$

Объяснение:

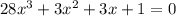
28x^3+3x^2+3x+1=0

разложение на множители):

Заметим, что данное уравнение хорошо раскладывается на множители:

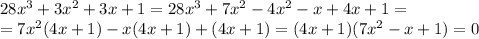
$28x^3+3x^2+3x+1=28x^3+7x^2-4x^2-x+4x+1=\\=7x^2(4x+1)-x(4x+1)+(4x+1)=(4x+1)(7x^2-x+1)=0$

Второй множитель не имеет корней.

Поэтом ответ 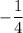$-\dfrac{1}{4}$ .

Поделим исходное уравнение на 28. Получим:

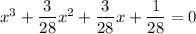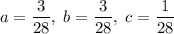
$x^3+\dfrac{3}{28}x^2+\dfrac{3}{28}x+\dfrac{1}{28}=0$ , где $a=\dfrac{3}{28},\;b=\dfrac{3}{28},\;c=\dfrac{1}{28}$

Выполним вычисления:

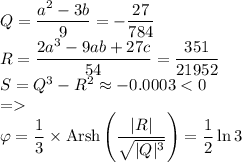
$Q=\dfrac{a^2-3b}{9}=-\dfrac{27}{784}\\R=\dfrac{2a^3-9ab+27c}{54}=\dfrac{351}{21952}\\S=Q^3-R^2\approx-0.0003\\\varphi =\dfrac{1}{3}\times \mathrm{Arsh}\left(\dfrac{|R|}{\sqrt{|Q|^3}}\right)=\dfrac{1}{2}\ln3$

Тогда действительный корень будет равен:

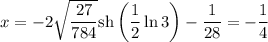
$x=-2\sqrt{\dfrac{27}{784}}\mathrm{sh}\left(\dfrac{1}{2}\ln 3\right)-\dfrac{1}{28}=-\dfrac{1}{4}$

Пришли к тому же ответу.

Уравнение решено!

(x²+4x)(x²+x-6)=(x³-16x)(x²-2x-35)

Раскроем скобки и упростим вырождение:

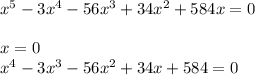
$x^5-3x^4-56x^3+34x^2+584x=0\\\\x=0\\x^4-3x^3-56x^2+34x+584=0$

Второе уравнение раскладывается на множители:

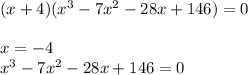
$(x+4)(x^3-7x^2-28x+146)=0\\\\x=-4\\x^3-7x^2-28x+146=0$

Последнее кубическое уравнение не имеет целых корней.

Поэтому нужно считать так же, как мы делали это при решении 1-ого уравнения 2-ым

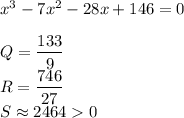
$x^3-7x^2-28x+146=0\\\\Q=\dfrac{133}{9}\\R=\dfrac{746}{27}\\S\approx24640$

Значит имеем 3 корня:

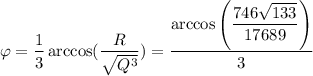
$\varphi=\dfrac{1}{3}\arccos(\dfrac{R}{\sqrt{Q^3}})=\dfrac{\arccos\left(\dfrac{746\sqrt{133}}{17689}\right)}{3}$

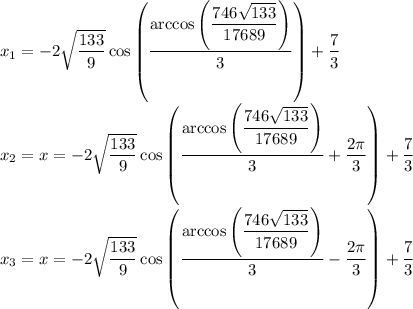
$x_1=-2\sqrt{\dfrac{133}{9}}\cos\left(\dfrac{\arccos\left(\dfrac{746\sqrt{133}}{17689}\right)}{3}\right)+\dfrac{7}{3}\\x_2=x=-2\sqrt{\dfrac{133}{9}}\cos\left(\dfrac{\arccos\left(\dfrac{746\sqrt{133}}{17689}\right)}{3}+\dfrac{2\pi}{3}\right)+\dfrac{7}{3}\\x_3=x=-2\sqrt{\dfrac{133}{9}}\cos\left(\dfrac{\arccos\left(\dfrac{746\sqrt{133}}{17689}\right)}{3}-\dfrac{2\pi}{3}\right)+\dfrac{7}{3}$