25 (км/ч)
Объяснение:
Расстояние против течения - Sпр.теч. = 100 км
Время против течения - tпр.теч. = 4часа
Расстояние по течению - Sпо теч. = 150 км
Время по течению - tпо теч. = 5 часов
На сколько км/ч скорость течения реки меньше собственной скорости лодки?
Пусть Vc. - собственная скорость лодки, а Vт. - скорость течения реки.
⇒ Vпо теч.=Vс. + Vт., Vпр.теч. = Vс. - Vт.
Чтобы найти скорость, нужно расстояние разделить на время:
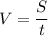
Найдем скорости по течению и против течения:
Vпр.теч. = 100:4 = 25 (км/ч)
Vпо теч. = 150:5 = 30 (км/ч)
Получим систему:
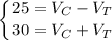
Сложим уравнения и найдем Vc.:
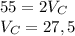
Собственная скорость лодки Vс.=27,5 км/ч
Найдем скорость течения реки:
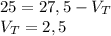 (км/ч)
(км/ч)
Найдем, на сколько км/ч скорость течения реки меньше собственной скорости лодки:
27,5 - 2,5 = 25 (км/ч)
y = (2x-1) / (x+3)
x = (2y-1) / (y+3) - выражаем теперь у через х:
x(y+3) = 2y - 1
y(2-x) = 3x+1
y = (3x+1) / (2-x) - обратная функция.
Теперь необходимо ее построить.
1) Найти точки экстремума и (или) точки перегиба:
y' = [3*(2-x) + (3x+1) ] / (2-x)^2 = [6-3x+3x+1] / (2-x)^2 = 7/(2-x)^2 - производная всегда положительная, значит функция у возрастает на всей области определения.
2) ОДЗ: 2-x # 0, x # 2. Значит прямая х=2 - ассимптота функции у.
3) Нули функции: y=0, 3x+1=0, x=-1/3. Точка (-1/3; 0).
4) Пересечение с осью Оу: х=0, у=1/2. Точка (0; 1/2)