Итак, мы ищем площадь фигуры, ограниченной линиями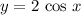 
, 
, 
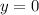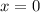и 
. Чертеж представлен ниже.
На чертеже видно, что на отрезке ![[0; \pi ]](/tpl/images/1257/1440/8b20f.png)
сверху может быть как и кривая 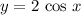, так и прямая 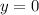. Поэтому можно посчитать интеграл на двух промежутках, а полученные значения сложить (таков один из возможных
Напоминаю также формулу Ньютона-Лейбница (и то, что "первообразная от косинуса равна синусу"):
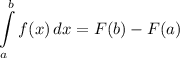
Первый промежуток: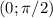 
. Кривая выше прямой, поэтому 
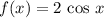. Нижний и верхний пределы - 
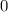и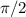 
соответственно.
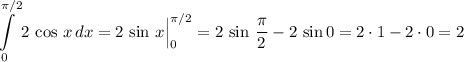
Второй промежуток: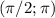 
. Так как 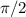такая точка, в которой косинус меняет свой знак, то и 
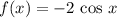. Имеем следующее (по идее, вторая площадь равна первой из-за периодичности косинуса, но проверить это тоже невредно):
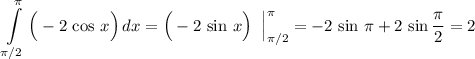
Значит, и вся площадь равна:
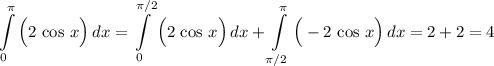
Задача решена!
ответ: 4.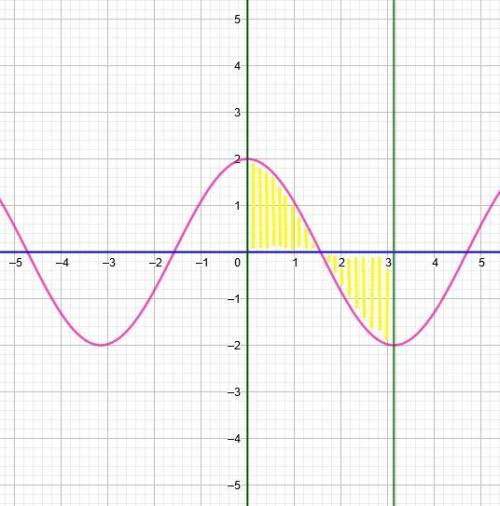
0<x<4/3
Объяснение:
числитель является положительным (это число 7, от x не завист)
надо найти значения x, при которых знаменатель положителен:
4 × x - 3 × x**2 > 0
4 × x - 3 × x**2 = x × (4 - 3×x)
рассмотрим 2 случая:
1. Оба положительные ( и x, и (4 - 3×x)): одновременно должно выполняться:
x > 0 и 4 - 3 × x > 0
x > 0 и -3×x > -4
x > 0 и x < 4/3
в этом случае решение существует. А именно,
0<x<4/3
2. Оба отрицательные: одновременно должно выполняться:
x < 0 и 4 - 3×x < 0
x < 0 и -3 × x < - 4
x< 0 и x> 4/3
в этом случае решения не существует.
Оставляем первый случай.