площа ромба дорівнює половині добутку його діагоналей, тоді
1)6помножити на 8 =48
2)48 поділити на 2 =24
1. Найти наибольшее и наименьшее значение функции
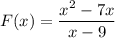на промежутке [-4; 1]
Точка разрыва x=9 в заданный интервал не входит.
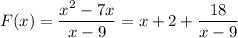
Первая производная для нахождения точек экстремумов.
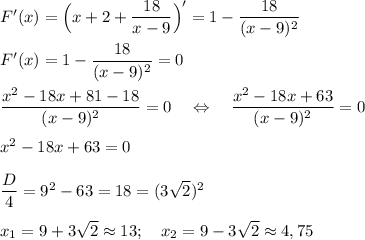
Обе точки экстремумов не попадают в интервал x∈[-4; 1]
Значения функции на концах интервала
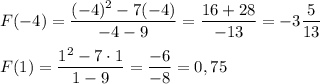
ответ: наименьшее значение функции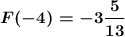 
;
наибольшее значение функции F(1) = 0,75
-----------------------------------------------------------------------------
2. Записать уравнение касательной к графику
функции F(x)=x⁴-2x в точке x₀=-1
Уравнение касательной имеет вид y = F(x₀) + F’(x₀)·(x - x₀)
F(-1) = x⁴-2x = (-1)⁴ - 2(-1) = 1+2 = 3
F'(-1) = (x⁴-2x)' = 4x³ - 2 = 4(-1)³ - 2 = -6
y = F(x₀) + F’(x₀)·(x - x₀) = 3 - 6 (x + 1) = 3 - 6x -6 = -6x - 3
ответ: уравнение касательной y = -6x - 3
---------------------------------------------------------------------------
3. Исследовать функцию и построить ее график F(x)=x³-3x²
1) Область определения D(F) = R
2) Область значений E(F) = R
3) Нули функции
F(x)=x³-3x² = 0; x²(x - 3) = 0; x₁ = 0; x₂ = 3
4) Пересечение с осью OY
x = 0; F(0) = 0³-3·0² = 0
5) Экстремумы функции
F'(x) = 0; (x³-3x²)' = 0; 3x² - 6x = 0; 3x(x - 2) = 0;
x₁ = 0; F(0) = 0; F"(0) = 6x - 6 = -6 ⇒ локальный максимум.
x₂ = 2; F(2) = 2³-3·2² = -4; F"(2) = 6x - 6 = 6 ⇒ локальный минимум.
6) Монотонность функции.
Интервалы знакопостоянства первой
производной F'(x) = 3x(x - 2)
++++++++ (0) ------------- (2) +++++++++> x
/ \ /
x ∈ (-∞; 0)∪(2; +∞) - функция возрастает
x ∈ (0;2) - функция убывает
7) Функция не периодическая, общего вида (не является чётной, не является нечётной).
8) Дополнительные точки для построения
x₃ = -1; y₃ = -4; x₄ = 1; y₄ = -2
9) График функции в приложении
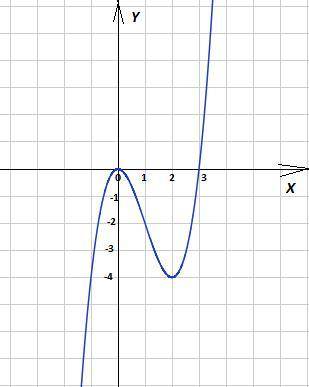
Объяснение:
S=1/2*d1*d2=1/2*6*8=48/2=24