10 ед. изм.
Объяснение:
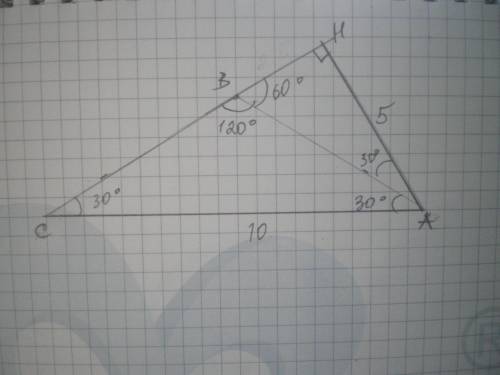
Дано: ΔАВС - равнобедренный, АВ=ВС, ∠В=120°, АН=5. Найти АС.
В тупоугольном треугольнике высота падает на продолжение противоположной стороны.
∠ВАС=∠С=(180-120):2=30°
В ΔАВН - прямоугольном ∠АВН=180-120=60°, тогда ∠ВАН=90-60=30°.
∠А=30+30=60°
В ΔАСН - прямоугольном ∠С=30°, тогда АС=2АН=5*2=10 (ед. изм.)
Для того, чтобы найти сумму первых двадцати членов арифметической прогрессии заданной формулой n - го члена прогрессии an = 3n + 2 прежде всего вспомним формулу для нахождения суммы n первых членов арифметической прогрессии.
Sn= (a1 + an)/2 * n.
Из заданной формулы найдем первый и двадцатый член арифметической прогрессии:
a1 = 3 * 1 + 2 = 3 + 2 = 5;
a20 = 3 * 20 + 2 = 60 + 2 = 62.
Теперь можем подставить найденные значения в формулу для нахождения суммы и произвести вычисления.
S20= (a1 + a20)/2 * 20 = (5 + 62)/2 * 20 = 67/2 * 20 = 67 * 10= 670.
Объяснение:
Система уравнений:
x + 5y = 7;
3x + 2y = -5.
Выражаем из первого уравнения системы переменную x через у и получаем следующую систему уравнений:
x = 7 - 5y;
3x + 2y = -5.
Теперь подставим во второе уравнение системы вместо x выражение из первого уравнения системы:
x = 7 - 5y;
3(7 - 5y) + 2y = -5.
Переходим к решению второго уравнения системы:
3 * 7 - 3 * 5y + 2y = -5;
21 - 15y + 2y = -5;
-15y + 2y = -5 - 21;
-13y = -26;
y = -26 : (-13);
y = 2.
Система уравнений:
x = 7 - 5y = 7 - 5 * 2 = 7 - 10 = -3;
y = 2.
ответ: (-3; 2).
Объяснение:
<С=(180-120):2
<С=30
2) рассмотрим треугольник AA1C - прямоугольный, т.к. AA1-высота, <AA1C=90
<С=30, значит
AA1=1/2AC, т.к. напротив угла в 30 градусов лежит катет, равный половине гипотенузы.
AC=2*AA1
AC=10
ответ: 10