Ну, уравнение очень нелегкое. Без калькулятора не решить:)))
Пусть всего было х шаров. До начала представления после продажи осталось
х-0,09375*х шаров. Это проценты перевели в десятичную дробь, разделив проценты на 100 по определению. Получается. что осталось 0,90625*х - шаров. В антракте продают 6/23 этих оставшихся шаров. 1-6/23=17/23 - осталось. Значит 17/23 *0,90625*х шаров осталось после антракта.
Теперь по условию задачи это число меньше, чем х на 243 шара. Составим уравнение
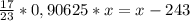
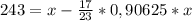
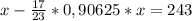
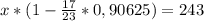
Приведем к общему знаменателю
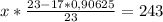
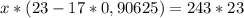
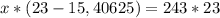
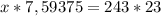
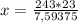
x=736 - шаров было вначале у продавца
А дальше находим корни этого уравнения, принадлежащие указанному отрезку:
Косинус равен единице только в точках х = 0 и х = 2П (из указанного промежутка).
На указанном отрезке [0; 2П] синус принимает наименьшее значение в точке "3 пи пополам", равное (- 1), а наибольшее - в точке "пи пополам", равное (+ 1).
Косинус на этом отрезке монотонно убывает от ) до П, (наименьшее значение, принимаемое косинусом на данном промежутке, равно - 1) и монотонно возрастает от П до 2П, где вновь принимает максимальное значение, равное +1.
Вычисляйте значения в концах отрезка:
х = 0 у = 0 - 0 = 0 - наименьшее значение.
х = 2П у = 2П - 0 = 2П - наибольшее значение
у=2х у=-3 у=2х-1
2х=0 х=0 2х-1=0
2х=1 2х=1
х=0 (0;-3) х=0,5
у=2*0 у=2*0,5-1
у=0 у=0
(0;0) (0,5;0)
Объяснение: