√х+5=-2/х; Левая часть уравнения - это функция у=√х+5, которую можно построить путем сдвига графика функции у=√х на 5 единиц вверх вдоль оси ординат (OY). Можно построить по точкам, например: х 0 1 4 9 у 5 6 7 8 Правая часть уравнения - это обратная пропорциональность. Можно построить по точкам, например: х -4 -2 -1 -1/2 1/2 1 2 4 у 1/2 1 2 4 -4 -2 -1 -1/2 Графики см. на рисунке 1. На рисунке видно, что у этого уравнения нет решения, так как первый график расположен в первой четверти, а второй график - во второй и четвертой, т.е. они не имеют общих точек, не пересекаются. ответ: нет корней.
Если Вы имели ввиду уравнение √(х+5)=-2/х, то левую часть можно построить путем сдвига графика функции у=√х на 5 единиц влево вдоль оси абсцисс (ОХ), или по точкам, например: х -5 -4 -1 4 у 0 1 2 3 Правую часть строим также, как и в предыдущем примере. См. рисунок 2. На рисунке видно, что решением уравнения является точка пересечения графиков при х=-1. ответ: -1.
2) {3x+4y=-1 Тут всё нужно умножить на -2, чтобы потом избавиться от x 2x+5y=4 Тут всё нужно умножить на 3, чтобы потом избавиться от X АНАЛОГИЧНО ПЕРВОМУ: {-6x-8y=2 6x+15y=12
1. x^2-4x+40≤0
D = b^2−4ac = 16-160 = -144
D < 0 ⇒ нет корней
Т.к. a = 1 > 0, то x^2−4x+40 > 0 для любых x, следовательно, неравенство x^2-4x+40 ≤ 0 не имеет смысла.
ответ: x∈∅, решений нет.
2. x^2-4x+40<0
Аналогично, как для п 1.
Т.к. a = 1 > 0, то x^2−4x+40 > 0 для любых x, следовательно, неравенство x^2-4x+40 < 0 не имеет смысла.
ответ: x∈∅, решений нет.
3. x^2-4x+4>0
D = 16-16 = 0
D = 16-16 = 0 ⇒ 1 корень
x = -b/2 = 4/2 = 2
Вычислим знаки на каждом интервале:
x<2 | x>2
+ | +
Неравенство строгое, значит точка с абсциссой x=2 — выколотая.
ответ: x∈(−∞; 2)∪(2; +∞) или x<2; x>2.
4. x^2-4x+4≥0
x = 2 (см п. 3.)
Вычислим знаки на каждом интервале:
x<2 | x>2
+ | +
Неравенство нестрогое, значит точка с абсциссой x=2 — входит в решение.
ответ: x∈(−∞; +∞) или x — любое число, x∈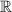 .
.