![1)\sqrt[5]{7\frac{19}{32}}=\sqrt[5]{\frac{243}{32} }=\sqrt[5]{(\frac{3}{2})^{5}} =\frac{3}{2}=1,5\\\\2)\sqrt{5\frac{4}{9}}=\sqrt{\frac{49}{9}}=\sqrt{(\frac{7}{3})^{2}}=\frac{7}{3}=2\frac{1}{3} \\\\3)\sqrt[3]{\frac{8b^{6}}{343a^{9} }}=\sqrt[3]{(\frac{2b^{2}}{7a^{3}})^{3}}=\frac{2b^{2} }{7a^{3}}](/tpl/images/1235/3305/fe068.png)
![4)\sqrt[4]{\frac{16x^{8}}{81y^{4}}}=\sqrt[4]{(\frac{2x^{2}}{3y})^{4}}=\frac{2x^{2}}{3y}\\\\5)3\sqrt{20}+7\sqrt{15}-\sqrt{5}):\sqrt{5} =\frac{3\sqrt{4*5}+7\sqrt{3*5}-\sqrt{5}}{\sqrt{5}}=\frac{\sqrt{5}(3*2+7\sqrt{3}-1)}{\sqrt{5}}=5+7\sqrt{3}\\\\6)(\sqrt[3]{7}-\sqrt[3]{14}+\sqrt[3]{56}):\sqrt[3]{7}=\frac{\sqrt[3]{7}-\sqrt[3]{7*2}+\sqrt[3]{7*8}}{\sqrt[3]{7}}=\frac{\sqrt[3]{7}(1-\sqrt[3]{2}+2)}{\sqrt[3]{7}}=3-\sqrt[3]{2}](/tpl/images/1235/3305/e76dd.png)
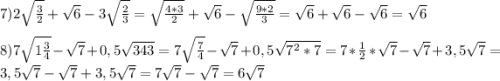

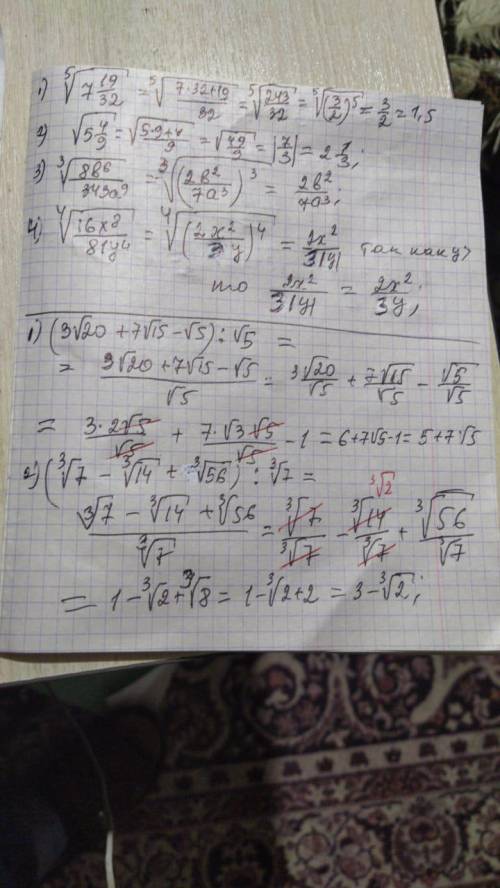
ответ: приложено
Объяснение:
Объяснение:
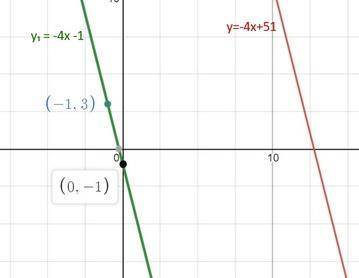
если известно, что искомая прямая y₁ = k₁x +b₁ параллельна прямой y=-4x+51 (у=кх +b), то мы знаем коэффициент k₁ = -4 при x, т.к. у параллельных прямых коэффициенты k и к₁ при х равны.
тогда мы уже имеем "половину" уравнения у₁ = -4х +b₁
теперь для определения b₁ используем то, что искомая прямая проходит через точку M(-1; 3). это означает, что координаты точки должны удовлетворять уравнению у₁ = -4х +b₁. подставим эти координаты
3= -4*(-1) +b₁ тогда b₁ = -1
и искомое уравнение
у₁ = -4х -1
теперь проверим, принадлежит ли построенному графику точка N(-50; 200). подставим ее координаты в уравнение у₁ = -4х -1
200 ≠ -4*(-50)-1
точка N(-50; 200) ∉ графику функции у₁ = -4х -1
тогда строим график по двум точкам
х = -1 у₁(-1) = 3 точка M(-1; 3)
х = 0 у₁(0) = -1
на первом фото построение по двум точкам у₁ = -4х -1 ║y=-4x+51
на втором показано, что точка N(-50; 200). ∉ графику у₁ = -4х -1