Р пр-ка = 60 м
Sдор. = 64 м²
шир. дор. = ? м
Решение.
Если а и b - длина и ширина, соответственно, м, то
Рпр-ка = 2а + 2b ---- периметр здания
х, м ---- ширина дорожки
Площадь дорожки складывается из 8 участков, Двух равных по длине длине здания, двух равных по длине ширине здания и четырех квадратов по углам, со стороной равной стороне дорожки.
Sдор. = 4х² + 2ах + 2bх = 4х² + х(2а + 2b) = 4х² + х*Рпр-ка
4х² + 60х = 64 ----- по условию | : 4
х² + 15х - 16 = 0
D = 15² + 4*16 = 225 + 64 = 289 = 17²
х₁ =(-15 + √17²)/2 = (-15+17)/2 = 1 (м) ----- ширина дорожки
х₂ = (-15 - 17)/2 = - 16 м -- отбрасываем, как посторонний корень, не имеющий физического смысла
ответ: 1 м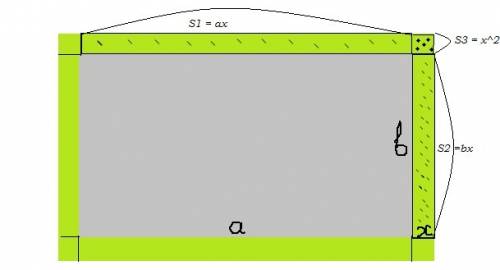
![lim_{x\to \infty }\frac{x+1}{x-2}=lim_{x\to \infty }\frac{\frac{x}{x}+\frac{1}{x}}{\frac{x}{x}-\frac{2}{x}}=lim\frac{1+\frac{1}{x}}{1-\frac{2}{x}}=[\frac{1+0}{1-0}]=\frac{1}{1}=1](/tpl/images/0237/6916/b2fde.png)
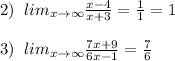
![lim_{x\to \infty }\frac{x+3}{5x^2+2x-5}=0,tak\; \; kak\\\\lim_{x\to \infty }\frac{\frac{x}{x^2}+\frac{3}{x^2}}{\frac{5x^2}{x^2}+\frac{2x}{x^2}-\frac{5}{x^2}}=lim\frac{\frac{1}{x}+\frac{3}{x^2}}{5+\frac{2}{x}-\frac{5}{x^2}}=[\frac{0+0}{5+0-0}]=\frac{0}{5}=0](/tpl/images/0237/6916/32e6e.png)
По модулю очень громоздко. Всё же напишу очень простое доказательство.
Известный факт а^n-1 делится нацело на (а-1). Тем не менее докажем его по индукции. Для n=1 фаакт верен. Пусть верен для n-1
Но а^n-1=а*(а^(n-1)-1)+(а-1) по предположению индукции первое слагаемое на (а-1) делится, второе тоже.
Но 6^240-1=36^120-1 и значит делится на (36-1)=35, что и требуется.