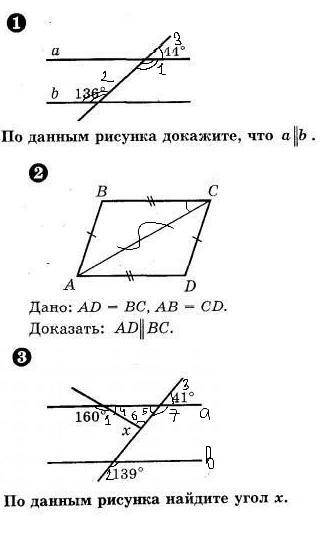
1. ∠1 и ∠3 смежные, значит ∠1 = 180° - ∠3 = 180° - 44° = 136°
∠1 и∠2 внутр. накрест лежащие углы, они равны между собой по 136° => a параллельно b
2. рассмотрим ΔABC и ΔADC.
они равны по 3 признаку, так как AC общая сторона, AD = BC и AB = CD
∠BCA = ∠DAC (как внутр. накрест лежащие углы), а из этого следует, что AD параллельно BC
3. обозначим на рисунке ∠4, ∠5, ∠6 и ∠7
∠7 = 180° - ∠3 = 180° - 41° = 139°, следовательно ∠7 = ∠3, значит a параллельно b
∠5 = ∠3 = 41° (как вертикальные)
∠4 = 180° - ∠1 = 180° - 160° = 20°
и ∠6 = 180° - ∠4 - ∠5 = 180° - 20° - 41° = 119°
следовательно угол, обозначенный как x, равен 180° - ∠6 = 180° - 119° = 61°
1. a)5 < m < 15; 5*1/5 < 1/5 m < 15*1/5; 1 < 1/5 < 3
b) 5 < -2m < 15; 5*(-2) < -2m < 15*(-2); -10 < -2m < -30; -30 < -2m < -10
c) 5 < m-6 < 15; -5+6 < m-6 < -15+6 ; 1 < m-6 < -9; -9< m-6 < 1
2. a) 2.6 <√7 <2.7; 2.6*2 < 2√7 < 2.7*2 ; 5.2 < √7 < 5.4
b)- 2.6 <-√7 < -2.7; -2,7 < -√7 < -2,6
c) 2.6 <√7 <2.7; 2+2.6 < 2+√7 < 2+2.7; 4.6 < √7 < 4.7
d)2.6 <√7 <2.7; 3-2.6 < 3-√7 <3-2.7; 0.4 <;3-√7 <0.3; 0.3 < 3-√7 < 0.4