Примем одну сторону как "х", другую как "у". Составляем систему уравнений (цифры с двоеточием заменить фигурной скобкой)
1: х - у = 14
2: х^2 + y^2 = 26^2
Получаем, что:
х = (14 + у)
(у^2 + 28y + 196) + y^2 = 676
Приводим подобные:
2y^2 + 28y - 480 = 0
Сокращаем на "2":
y^2 + 14y - 240 = 0
Далее решаем по теореме Виета для квадратных уравнений, либо через дискриминант (лично я предпочитаю второе):
a = 1, b = 14, c = -240
D = b^2 - 4ac
D = 14*14 + 4*240 = 1156
√D = 34
у1 = -b+√D/2a = -14+34/2 = 10 см.
y2 = -b-√D/2a = -14-34/2 = -24 см (таких сторон прямоугольников не существует в природе, вычеркиваем =)).
Подставляем в первое уравнение х = (14 + у) и... о чудо!:
14+10 = 24 см.
ответ: Большая сторона данного прямоугольника равна 24 сантиметрам.
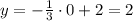
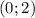
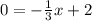
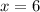
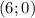
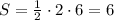
1)
у=2х+1
у=2х-3
у=х+7
Эти линейные функции вида у=kx+b, где k-это угловой коэффициент, с его изменением будет меняться угол наклона прямой к оси Ох, значит, функции с одинаковыми угловыми коэффициентами будут параллельны друг другу. Отсюда параллельные функции:
у=2х+1 и у=2х-3. Эти графики функций можно построить по двум точкам каждый. Находим точки:
у=2х+1
х=0
у=2*0+1=0+1=1
(0;1)
х=1
у=2*1+1=3
(1;3)
у=2х-3
х=0
у=2*0-3
у=-3
(0;-3)
х=1
у=2*1-3=-1
(1;-1)
у=х+7
х=0
у=7
(0;7)
х=2
у=2+7=9
(2;9)
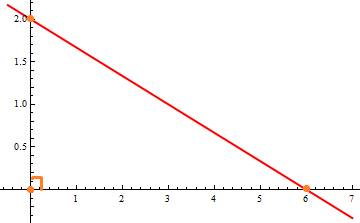
По этим точкам строим графики.
2)
Поскольку графики прямые, два из которых параллельны, то эти 2 графика будут пересекать третий, т.е. у=2х+1 и у=2х-3 будут пересекать график у=х+3, а график у=х+7 пересекать его не будет, т.к. он с тем же угловым коэффициентом.
Для нахождения координат пересечения приравняем функции:
2х+1=х+3
2х-х=3-1
х=2
у=2+3=5
координата пересечения (2;5)
2х-3=х+3
2х-х=3+3
х=6
у=6+3=9
(6;9)
Объяснение: