ответы на тест:
1) (14/13−11/12)⋅10/11ответ:
125/ 858
2) Разложи на множители: x^2+2xy+y^2.ответ:х+у^2
3) Вычисли: (−4/5)^4−(1/25)^2+18 ответ:18 51/125
4)Представь в виде произведения x10y20−1.ответ:(x^5y^10−1)⋅(x^5y^10+1)
5)Разложи на множетели:p^3−p^2k−pk^2+k^3ответ:(p-k)^2*(p+k)
6) Используя правила умножения и деления степеней, упрости выражение:b^7⋅b^13 / b^19 ⋅ z^56⋅z^9 / z64ответ:b * z (умножить)
7) Упрости:(t2)^2−(t2)^7⋅(t2)^6:(t2)^13
ответ: *их два*1/4 t^2−1
t2/4 −1
Ну и последний это -4а)
Всем УДАЧИ) у меня 5)
пусть а - сторона основания, а l - апофема, тогда формула площади поверхности конуса равна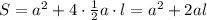
Подставим вместо а и S их значения и найдем апофему l
Через апофему проведем сечение пирамиды. В сечении получаем равнобедренный треугольник, основание которого равно стороне а=5, а боковые стороны апофеме l=6. Угол между боковой стороной треугольника и его основанием и есть угол наклона боковой грани пирамиды к плоскости основания. Найдем его, проведем высоту в равнобедренном треугольнике к его основанию. Высота равнобедренного треугольника, проведенная к основанию является так же его биссектрисо и медианой. Поэтому она делит равнобедренный треугольник на два равных прямоугольных треугольника. Найдем косинус искомого угла из прямоугольного треугольника.
Cos A=2,5/6=25/60=5/12 Отсюда следует, что угол наклона боковой грани к плоскости основания пирамиды равен arccos (5/12)