7/Задание № 4:
Назовите такое значение параметра a, при котором неравенство ax>7x+2 не имеет решений.
ax>7x+2
ax-7x>2
(a-7)x>2
Если а=7, то неравенство 0>2 не имеет решений.
Если а>7, то решения x>2/(a-7)
Если а<7, то решения x<2/(a-7)
ОТВЕТ: 7
7/Задание № 3:
Сколько корней имеет уравнение: |x+2+|−x−4||−8=x?
|x+2+|−x−4||−8=x
|x+2+|x+4||−8=x
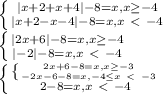
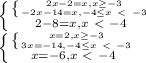
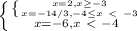
Условию раскрытия моделей соответствуют только первый и третий корни 2 и -6.
ОТВЕТ: 2 корня
7/Задание № 1:
Сколько чётных двузначных чисел, которые при делении на сумму цифр числа дают неполное частное 7 и остаток 3?
РЕШЕНИЕ: Пусть это число АВ=10a+b. Тогда, 10a+b=7(a+b)+3.
10a+b=7a+7b+3
3a=6b+3
a=2b+1
2b=a-1
Учитывая, что:
- а и b цифры, то есть целые числа от 0 до 9, но а не ноль, поскольку AB двузначное число
- число AB должно быть четным, то проверять нечетные b нет смысла
- остаток должен быть меньше делителя, значит минимально возможная сумма (a+b) равна 4
b=0: a=2*0+1=1 - не может быть a+b=1<4
b=2: a=2*2+1=5, число 52
b=4: a=2*4+1=9, число 94
При b=6 и более а=2*6+1=13 и более - не соответствует цифре.
ОТВЕТ: 2 числа
x= 4+ y;
Підставимо це значення x в друге рівняння:
(4+ y)²+ y²= 8;
Розкриємо дужки за формулами скороченого множення:
[(a+ b)²= a²+ 2ab+ b²]
16+ 8y+ y²+ y²- 8= 0;
2y²+ 8y+ 8= 0; | : 2
Поділимо на два всі коефіціенти:
y²+ 4y+ 4= 0;
[Маємо квадратне рівняння типу ax²+ bx+ c= 0]
Далі за дискримінантом:
D= b²- 4ac= 4²- 4* 1* 4= 0;
[Якщо дискримінант дорівнює 0, то рівняння має два співпадаючих кореня, тобто по факту один корінь]
y=
Якщо рівняння зведене (a= 1), можемо робити за теоремою Вієта:
y₁* y₂= c;
y₁+ y₂= -b;
В даному випадку:
y₁* y₂= 4;
y₁+ y₂= -4.
y= -2.
Підставимо значення y в перше рівняння та знайдемо x:
x+ 2= 4;
x= 4- 2= 2.