Объем правильного тетраэдра равен:
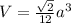
Так как ребро второго больше на 3 первого, возведем его в третью степень: 3³ = 27, и умножим на объем первого тетраэдра: 27*2 = 54
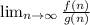 - где f(n) и g(n) многочлены.
- где f(n) и g(n) многочлены.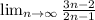 - здесь в числителе, старшая степень 3n. А в знаменателе 2n.
- здесь в числителе, старшая степень 3n. А в знаменателе 2n.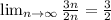
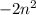 а в знаменателе n².
а в знаменателе n².
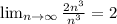
Объем тетраэдра равен
V=√2*a^3/12
при v=2 будем иметь
2=√2*a³/12=> 24=√2*a^3 => a^3=24/√2=√288 =>a=∛(√288)
при a=3*∛(√288) будем иметь
V=√2*(3*∛(√288))^3/12=27*√2*√288/12=27*√576/12=27*24/12=54