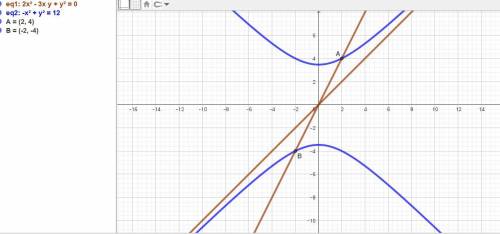
Дана система уравнений:
{2x² - 3xy + y² = 0,
{y² - x² = 12.
Из второго уравнения получаем y² = x² + 12 и подставим в первое.
2x² - 3xy + x² + 12 = 0,
3x² - 3xy + 12 = 0, сократим на 3:
x² - xy + 4 = 0
x(x - y) = -4 отсюда x - y = -4/x или y - x = 4/x.
Второе уравнение разложим как разность квадратов.
y² - x² = (y - x)(y + x) = 12.
Разделим почленно 2 уравнения.
(y - x)(y + x) = 12.
y - x = 4/x, получим y + x = 12/(4/x) = 3x или y = 3x - x = 2x.
Подставим во второе уравнение.
(2x)² - x² = 12,
4x² - x² = 12,
3x² = 12. x = +-√(12/3) = +-√4 = +-2.
y = 2x = 2*(+-2) = +-4.
ответ: x1 = -2, x2 = 2.
y1 = -4, y2 = 4.
a3 + a9 = a1 + 2d + a1 + 8d = 2a1 + 10d = 6
a1 + 5d = 3
a1 = 3 - 5d
a3*a9 = (a1+2d)(a1+8d) = a1^2 + 10a1*d + 16d^2 = 135/16
Подставляем 1 уравнение во 2 уравнение
(3-5d)^2 + 10(3-5d)*d + 16d^2 = 135/16
25d^2 - 30d + 9 + 30d - 50d^2 + 16d^2 = 135/16
Приводим подобные и умножаем все на 16
-9*16d^2 + 9*16 = 135
Переносим d^2 направо, а 135 налево
144 - 135 = 144d^2
d^2 = 9/144 = 1/16
Это уравнение имеет два корня
1) d = -1/4; a1 = 3 - 5d = 3 + 5/4 = 17/4
а3 = a1 + 2d = 17/4 - 2/4 = 15/4
a9 = a1 + 8d = 17/4 - 8/4 = 9/4
a15 = a1 + 14d = 17/4 - 14/4 = 3/4
S(15) = (a1+a15)*15/2 = (17/4 + 3/4)*15/2 = 20/4*15/2 = 75/2
2) d = 1/4; a1 = 3 - 5d = 3 - 5/4 = 7/4
a3 = 7/4 + 2/4 = 9/4; a9 = 7/4 + 8/4 = 15/4
a15 = 7/4 + 14/4 = 21/4
S(15) = (a1+a15)*15/2 = (7/4 + 21/4)*15/2 = 28/4*15/2 = 105/2
ответ: 75/2=37,5 или 105/2=52,5
Объяснение:
Листай картинки по порядку, надеюсь все понятно)