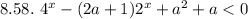
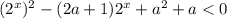
Замена: 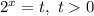
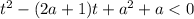
Имеем квадратичную функцию 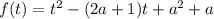 , графиком которой является парабола с ветвями, направленными вверх.
, графиком которой является парабола с ветвями, направленными вверх.
Найдем возможные точки пересечения параболы с осью абсцисс.
Для этого решим квадратное уравнение:
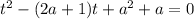
Найдем дискриминант данного уравнения:
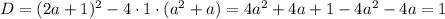
Имеем 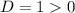 , значит данное уравнение имеет ровно 2 корня:
, значит данное уравнение имеет ровно 2 корня:
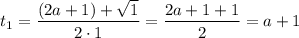
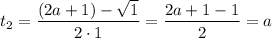
Имеем две точки пересечения параболы с осью абсцисс.
Пусть  . Тогда
. Тогда  . Имеем неверное неравенство. Следовательно, при всех значениях параметра
. Имеем неверное неравенство. Следовательно, при всех значениях параметра  имеем
имеем 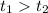 .
.
Тогда квадратичная функция 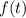 будет меньше 0 при
будет меньше 0 при 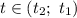
Последнее можно записать так:

Обратная замена:
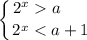
Если 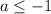 , то имеем:
, то имеем: 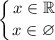
Решением такой системы неравенств является 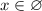
Если 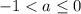 , то имеем:
, то имеем: 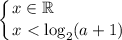
Решением такой системы неравенств является 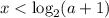
Если 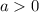 , то имеем:
, то имеем: 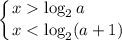
Решением такой системы неравенств является интервал 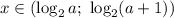
![a \in (-\infty; \ -1]](/tpl/images/1357/0229/00410.png) , то нет корней;если
, то нет корней;если ![a \in (-1; \ 0]](/tpl/images/1357/0229/7e5c2.png) , то
, то 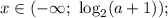 если
если 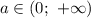 , то
, то 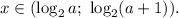
16/(х*х)=х-1
x^3-x^2-16=0
Извините, сначала написал неверное решение. У этого кубического уравнения 1 действительный корень х примерно равен 2,901.
То что корень примерно равен 3 вытекает из того, что х=3
корень уравнения x^3-x^2-18=0 . Тогда графически нетрудно понять куда смещается корень, когда меняется свободный член.
Точное решение ( с формулами Кардано) очень громоздко.
Может быть все же уравнение выглядит так (?):
4/х=sqrt(x)-1
Тогда, очевидно х=4 -решение.
Как это получить?
Обозначим sqrt(x)=у
4/(у*у)=у-1
y^3-y^2-4=0
(y^3-8)-(y^2-4)=0
(y-2)*(y^2+2y+4)-(y-2)*(y+2)=0
у=2 -решение. Пусть у не равен 2.
у^2+y+2=0
(y+0,5)^2+1,75=0
У этого уравнения нет решений.
Значит корень один у=2.
У исходного уравнения корень х=4.