Из 9 солдат нужно выбрать некоторых 7. Число сделать это равно числу сочетаний из 9 элементов по 7:
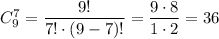
Из 6 сержантов нужно выбрать некоторых 4. Число сделать это равно числу сочетаний из 6 элементов по 4:
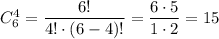
Из 4 офицеров нужно выбрать некоторого 1. Число сделать это равно числу сочетаний из 4 элементов по 1:
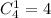
Так как выбор солдат, выбор сержантов и выбор офицера попарно независимы, то соответствующие нужны перемножить. То есть любому выбору солдат мы можем сопоставить любой выбор сержантов, а также любой выбор офицера.
Общее число вариантов:
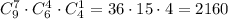
ответ: 2160 вариантов
1 этап: Составление математической модели.
Производительность ученика х деталей в час
из условия производительность мастера х+15 деталей в час
Мастер работал 6 час. значит изготовил 6*(х+15) деталей
Ученик работал 8 час. значит изготовил 8*х деталей
По условию мастер изготовил деталей в 3 раза больше
Таким образом 6*(х+15)=3*8*х
2 этап: Работа с составленной моделью
6(x+15)=24x | :6
(x+15)=4x
15=3x
x=5
3 этап: ответ на вопрос задачи.
За х мы обозначили производительность ученика и она равна 5 дет/час
значит производительность мастера 5+15=20 дет/час
Мы ответили на вопрос задачи.
Производительность мастера 20 дет/час
Пусть x км/ч - cобственная скорость катера.
v км/ч - скорость течения реки
Тогда
(x+v) км/ч - скорость катера по течению
(x-v) км/ч - скорость катера против течения
Cистема уравнений
\left \{ {{\frac{44}{x+v} + 3=\frac{90}{x-v}} \atop {\frac{66}{x+v} + \frac{54}{x-v}=6}} \right.{
x+v
66
+
x−v
54
=6
x+v
44
+3=
x−v
90
{44(x-v)+3(x-v)(x+v)=90(x+v)
{66(x-v)+54(x+v)=6(x-v)(x+v)
{3x²-3v²=46x+134v
{6x^2-6v^2=120x-12v
2·(46х+134v)=120х-12v
28x=280v
x=10v
собственная скорость катера в 10 раз больше скорости течения реки
Подставляем в первое уравнение:
44·(10v-v)+3·(10v-v)·(10v+v)=90·(10v+v);
44·9v+3·9v·11v=90·11v
Сокращаем на 99v
4+3v=10
3v=6
v=2
x=20
О т в е т. 20 км в час - собственная скорость катера.
28:2=14 часов понадобится плоту, чтобы проплыть по реке 28 км