Объяснение:
у=7х-2х²+1. Расставим в порядке y=ax²+bx+c.
y=-2x²+7x+1.
Коэффициент а равен -2, то есть ниже нуля. Это значить что ветви параболы направлены вниз.
у=6-9х+3х². Расставим в порядке y=ax²+bx+c.
у=3х²-9х+6.
Коэффициент а равен 3, то есть больше нуля. Это значить что ветви параболы направлены вверх.
Объяснение:
1) f(x)=2e^x+3x² f'(x)=2e^x+6x
2) f(x)= x sinx. f'(x)= sinx+xcosx
3) у = (3х – 1)(2 – х) y'=3(2 – х)+(3х – 1)×(-1)=6-3x-3x+1=-6x+7
4) y=9x²-cosx y'= 18x+sinx
5) y=e^x-x^7 y'= e^x-7x^6
7) f '(1), f(x)=3x2-2x+1. f'(x)=6x-2; f'(1)=6-2=4
8) у = х²(3х^5 – 2) ; х0 = – 1. у' =(3x^7-2x²)'=21x^6-4x
y'(-1)=21+4=25
9) f '( ), f(x)=(2x-1)cosx=2cosx-(2x-1)sinx
10) f '(1), f(x)=(3-x²)(x²+6)= -2x(x²+6)+2x(3-x²) = -4x³ -6x
11) f '(1), f(x)=(x^4-3)(x²+2), f'(x)=3x³ (x²+2)+2x(x^4-3)=5x^5+6x³-6x
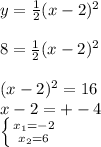
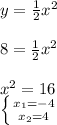
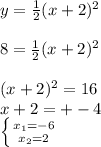
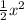 - расположен симметрично оси Y
- расположен симметрично оси Y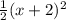 - график сдвинут по оси Х на 2 влево
- график сдвинут по оси Х на 2 влево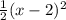 - график сдвинут по оси Х на 2 вправо
- график сдвинут по оси Х на 2 вправо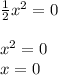
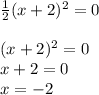
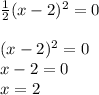
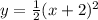 x∈
x∈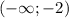
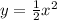 x∈
x∈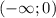
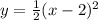 x∈
x∈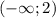
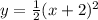 x∈
x∈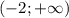
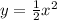 x∈
x∈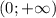
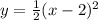 x∈
x∈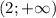
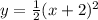 x=-2
x=-2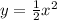 x=0
x=0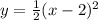 x=2
x=2
Если старший коэффициент, то есть коэффициент при x² положительный, то ветви параболы направлены вверх, а если отрицательный, то ветви направлены вниз.
1) y = 7x - 2x² + 1
y = - 2x² + 7x + 1
- 2 < 0 ⇒ ветви направлены вниз
2) y = 6 - 9x + 3x²
y = 3x² - 9x + 6
3 > 0 ⇒ ветви направлены вверх