Объяснение:
1) при x≥0 IxI=x
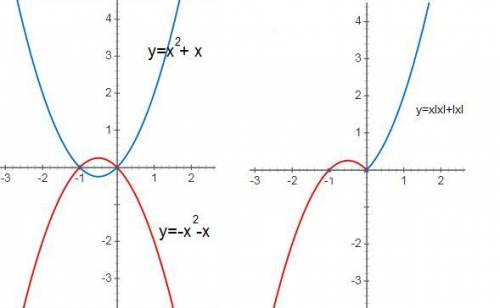
y=x²+x это парабола вершина в точке х=-b/2a=-1/2
y(-1/2)=0,25-0,5=-0,25
точки пересечения с осью ОХ x²+x=0 х(х+1)=0 х={-1;0}
строим график по эти точкам и оставляем только ту его часть где x≥0
2) при x<0 IxI=-x
y=-x²-x это парабола вершина в точке х=-b/2a=-1/2
y(-1/2)=-0,25+0,5=0,25
точки пересечения с осью ОХ -x²-x=0 -х(х+1)=0 х={-1;0}
строим график по эти точкам и оставляем только ту его часть где x<0
3) в задаче видимо имеется ввиду прямая у=m если так то
прямая у=m имеет с графиком одну общую точку при
m ∈(-∞;0)∪(0,25;+∞)
sin(7п+x)=cos(9п+2x)
sin(6п+п+x)=cos(8п+п+2x)
sin(п+x)=cos(п+2x)
-sinx=-cos2x
-sinx=sin^2x-cos^2x
-sinx=sin^2x-(1-sin^2x)
-sinx=sin^2x-1+sin^2x
2sin^2x+sinx-1=0
пусть sinx=y
2y^2+y-1=0
y=-1
y=1/2
Найдем х:
1)sinx=-1
x=-pi/2+2pik . k=z
2)sinx=1/2
x=(-1)^n *pi/6 +pik . k=z
sin^2(x/2)=cos^2 (7x/2)
0,5-0,5cosx=0,5+0,5cos7x
-cosx=cos7x
cos7x+cosx=0
2cos(7x+x)/2*cos(7x-x)/2=0
2cos4x*cos3x=0
2cos4x=0 или cos3x=0
4x=pi/2+pi*n 3x=pi/2+pi*n
x=pi/8+(pi*n)/4 x=pi/6+(pi*n)/3