Объяснение:
Последовательность называется возрастающей, если для любого n∈N выполняется неравенство yn<yn+1.
Последовательность называется убывающей, если для любого n∈N выполняется неравенство yn>yn+1.
Выпишем n-й и n+1-й члены последовательности: yn=n213n, yn+1=(n+1)213n+1.
Чтобы сравнить эти члены, составим их разность и оценим её знак:
yn+1−yn=(n+1)213n+1−n213n=(n2+2n+1)−13n213n+1=2n+1−12n213n+1
Для натуральных значений n справедливы неравенства 2n≤6n2 и 1<6n2.
Сложив их, получим 1+2n<12n2, т.е. для любых натуральных значений n справедливо неравенство 2n+1−12n213n+1<0, значит, yn+1−yn<0.
Итак, для любых натуральных значений n выполняется неравенство yn+1<yn,
а это значит, что последовательность (yn) убывает.
Зная автора задания как специалиста (в частности) в области геометрии, после первых неудачных попыток сделать эту задачу я подумал о возможности применить геометрию, после чего появилась надежда на успех.
Во-первых, мы можем считать, что x > 0 (если x<0, то y(x)>y(-x), то есть при отрицательном x наименьшее значение достигаться не может. Значение y(0)=6 пока просто запомним).
Пусть x>0 - некоторое число. Рассмотрим два . треугольника, один со сторонами 2 и x и углом в 30° между ними, второй - со сторонами 4 и x и углом в 90° между ними. Совместив их по стороне, равной x, получим 4-хугольник ABCD со сторонами AB=2, BC=4, диагональю BD=x и углом ABC, который диагональ BD делит на углы ABD=30° и DBC=90°. По теореме косинусов
Поэтому y(x) при положительном x - это сумма сторон AD и DС. Меняя x, мы меняем вершину D, двигая ее по лучу с вершиной B (при неподвижных A, B и C). Ясно, что сумма будет минимальной, когда четырехугольник ABCD вырождается (это когда D лежит на AC), и равна стороне AC,
Поскольку ответом в задаче будет
ответом в задаче будет 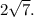
Замечание. Значение в нуле в принципе мы могли не вычислять, считая, что при этом получается вырожденный четырехугольник с нулевой диагональю.