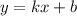я ничерта не понимаю
Три числа, перше з яких дорівнює 12, утворюють геометричну прогресію. Якщо від першого числа відняти 3, а друге і третє залишити без змін, то нова трійка чисел утворить арифметичну прогресію. Запишіть цю арифметичну прогресію

👇

Ответ:

новичок20030

09.05.2022

у нас ест 12 и 3 исходя из эти чисел и предоставленных мне услоивй я могу с точностью сказать,что ,чтобы решить эту не столь трудную задачу надо 12 разделить на 3

4,8(59 оценок)

Открыть все ответы

Ответ:

destroyer0800

09.05.2022

y=kx+b - уравнение прямой на координатной плоскости,

где - угловой коэффициент.

1) Известен угловой коэффициент первой прямой 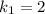k_1=2 .

2) Противоположная сторона квадрата лежит на прямой, параллельной первой прямой, а необходимым и достаточным условием их параллельности является равенство их угловых коэффициентов.

Получаем:

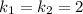
k_1=k_2=2

3) Две остальные стороны квадрата лежат на прямых, перпендикулярных первой прямой, а для этого необходимо и достаточно, чтобы их угловые были обратны по величине и противоположны по знаку.

Получаем:

$k_3=k_4=-\frac{1}{k_1}=-\frac{1}{2}=-0,5$

4) а теперь найдём сумму угловых коэффициентов трех прямых.

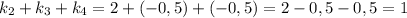
k_2+k_3+k_4=2+(-0,5)+(-0,5)=2-0,5-0,5=1

k_2+k_3+k_4=1

ответ: 1

4,7(30 оценок)

Ответ:

funnybotan2000

09.05.2022

Объяснение:

б) можно загнать под общий корень

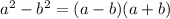твой пример $=\sqrt[7]{(5-\sqrt{26})(5+\sqrt{26}) }=$ по формуле сокращенного умножения a^2-b^2=(a-b)(a+b) = $\sqrt[7]{5^2-\sqrt{26}^2} =\sqrt[7]{25-26} =\sqrt[7]{-1} =$ так как корень нечетный можно выводить из под корня отрицательное число =

= $\sqrt[7]{-1} =-1$

в) по правилу $\sqrt[a]{b^n}=b^{\frac{n}{a} }$

$\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2} *\sqrt[3]{2}=\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2} *2^{\frac{1}{3} }=\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2} *2^{\frac{2}{6} }=\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2} *\sqrt[6]{4}$

коротко если говорить я сделал знаменатель равным 6-ти, чтобы объединить корни

$\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2} *\sqrt[6]{4}=\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2*4}=\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{8}$

вынесем минус

$-\sqrt[3]{2\sqrt{2} }+\sqrt[6]{8}= -\sqrt[3]{2\sqrt{2} }+\sqrt[3]{2\sqrt{2} }=0$

почему?

$\sqrt[6]{8}=\sqrt[6]{2*4}=\sqrt[6]{2*2^2}=\sqrt[6]{\sqrt{2}^2*2^2 } =\sqrt{2}^{\frac{2}{6} }*2^{\frac{2}{6} }= \sqrt{2}^{\frac{1}{3} }*2^{\frac{1}{3} }=\sqrt[3]{2\sqrt{2} }$

$-a+a=0\\a=\sqrt[n]{2\sqrt{3} }$

еще 2 примера

ну ладно

$\sqrt[4]{7+4\sqrt{3} } *\sqrt{2-\sqrt{3} }$

чтобы сделать под общий корень, нужно чтобы степень корней была одинакова

$=\sqrt[4]{(7+4\sqrt{3})((2-\sqrt{3})^2) } =$

формула сокращенного умножения

$\sqrt[4]{(7+4\sqrt{3})(4-4\sqrt{3}+3) }=\sqrt[4]{(7+4\sqrt{3})(7-4\sqrt{3})} =\sqrt[4]{49-48} =\sqrt[4]{1} =1$

тут всё знакомо с предыдущих

ну кроме того что $\sqrt{x} =\sqrt[2]{x}$ = $\sqrt[4]{x^2}$ = $x^{\frac{2}{4} }=x^{\frac{1}{2} }$

d) $\sqrt{3+\sqrt[4]{(-8)^2}} -\sqrt{3-\sqrt[4]{(-8)^2}}=\sqrt{3+\sqrt[4]{64}}-\sqrt{3-\sqrt[4]{64}}=\sqrt{3+\sqrt[4]{2^6}}-\sqrt{3-\sqrt[4]{2^6}}=\sqrt{3+2\sqrt{2} }-\sqrt{3-2\sqrt{2} }$