105. а > 12
106. РЕШЕНИЙ НЕТ
....
108. с = 2
Объяснение:
105.

Найти значения а, при которых
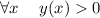
Графиком функции является парабола, ветви вверх. Необходимо вычислить такие значения а, при которых вершина параболы находится выше оси Ох.
Найдем через производную координату х точки минимума функции
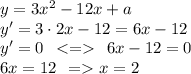
и координату у
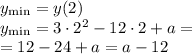
И найдем значения а, при которых у(мин) >0
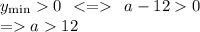
106. Решений нет. См. в фотографии.
Элементарно приводится контрпример.
Для любых значений а
значение функции при х = 0
будет равно 2 - т.е. положительное.
Что противоречит условиям
108.
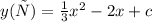
На самом деле здесь оптимально будет решить систему.
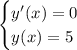
Но поступим иначе.
График функции - парабола, ветви вниз.
1) Минимальное значение у - в точке вершины параболы. Т.е. в точке, где производная функции равна 0:
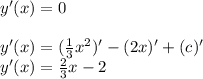
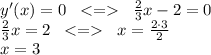
2) И в этой точке значение у Должно быть равно 5
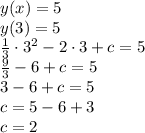
ответ: при с = 2

Фактически, мы можем сказать, что данный график - это парабола, ветки которой направленны вверх. Вершина параболы - это точка наименьшего значения уравнения, ее можно найти по данной формуле:
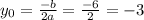 (наименьшее значение выражения)
(наименьшее значение выражения)
Подставив это значение, мы получим x₀ координату:
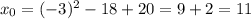 (значение переменной x, при самом наименьшем значении)
(значение переменной x, при самом наименьшем значении)
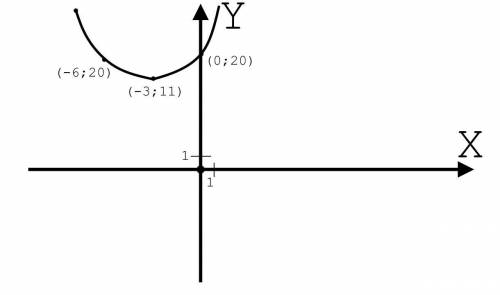
Для того, что бы доказать то, что значения всегда положительны достаточно построить график:
Мы уже знаем координаты вершины, потому нам следует всего лишь найти точку пересечения с осью ординат, подставив в уравнение вместо x, значения 0:
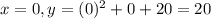
По аналогии, зная что данный график - это парабола можно подставить точку "-6"
Имея эти две точки мы можем построить график (прикреплённый файл).
По графику видно, что значения "y" - всегда положительны
Подробное решение в фото.