___________________
Удачи вам!!:))))
_____________________
1. Задайте линейную функцию, график которой параллелен графику данной линейной функции и проходит через данную точку М:
а) y = -5x, М(0; 3); k=-5 ; b=0
формула линейной функции
y=kx+b
т.М лежит на оси OY
b=3
k=-5
y=-5x+3
2. Задайте линейную функцию, график которой параллелен данной прямой и проходит через заданную точку N:
а)x - у + 3 = 0, N(0; 1);
x - у + 3 = 0 тоже самое, что y=x+3 k=1 ; b=3
формула линейной функции
y=kx+b
т.N лежит на оси OY
b=1
k=1
y=x+1 можно x - y + 1 = 0
б)-9x - Зу + 2 = 0, N(-2; 1).
-9x - Зу + 2 = 0
3y=-9x +2
y= -3x +2/3 k=-3 ; b=2/3
N(-2; 1) = (x1;y1)
подставим х1=-2 в -9x - Зу + 2 = 0
-9(-2) - Зу + 2 = 0
y=20/3
разница значений y-y1 = 20/3 -1 =20/3 -3/3 =17/3
тогда
b-b1=17/3 ; b1=b-17/3=2/3-17/3=-15/3=-5
k1=k=-3
y=-3x -5 можно -3x - y +5 =0
1) (X+2)*(X+3)
2) (X-2)*(X-3)
3) (X-5)*(X-3)
4) (X-3)*(X-4)
5) (X-4)*(X+3)
6)(X-4)*(X+2)
7) (X-3)*(X+2)
8) (X+5)*(X-3)
Ну во-первых, раскладывается квадратный трехчлен по формуле:
a(x- первый корень)*(х- второй корень)
Корни мы находим либо решая этот трехчлен как квадратное уравнение, либо по теореме Виета (удобнее, запись становится короче).
Я решала в основном по теореме(исключение - трехчлен под номером 6). В общем, теорема Виета:
сумма корней равна числу b,но с противоположным знаком (т.е. число b в формуле ax²+bx+c)
А произведение корней (x1*x2) равно числу c(знак не меняем!)
Через дискриминант решаем как обычное квадратное уравнение, т.е. выписываем ниже трехчлен уже как уравнение (проще говоря, приписываем =0 к концу трехчлена)
Объяснение:
а)по формуле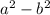
= (a-b)(a+b) =>
(x-0,9)(x+0,9)
б)по формуле
=
=>
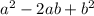в)по формуле из пункта а) =>
г)по формуле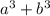
=
=>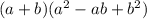