1. -1,4
2. Одночленом не является то выражение, части которого не разделяются плюсом или минусом (К примеру, 2abc будет одночленом, а ab + 2c не будет, в общем, ab + 2c будет многочленом), в данном случае ответом будет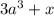 
3. Подобные слагаемые - те, которые имеют одну и ту же буквенную часть (Если одна буква возведена в одну степень, а другая в другую, они не будут подобными слагаемыми), при выполнении действий с ними, коэффициенты (Числа перед буквами) слагаются/вычисляются, в данном случае ответом будет 3a + 4b
4. При умножении одинаковых переменных степени слагаются, т.е., в данном случае будет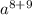 
= 
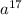
5. 
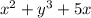, как решать, я уже объяснял
6. 4y + 5 (8y - (4y - 5) = 8y - 4y + 5, так как перед скобкой стоит минус, остальное я уже объяснял)
7. 16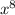
, так как, если после скобок стоит степень, степени внутри скобок умножаются на степень после скобок
8. 12x - 14 (Просто число перед скобками умножается на числа внутри скобок)
9. 
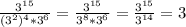(В конце степени просто сокращаются, и остается только 3)
10. 
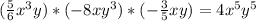(Коэффициенты сокращаются, и в итоге остается 
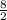, что равно 4, а результат положительный, так как отрицательное число, умноженное на отрицательное, становится положительным)
Середній рівень
У нас є дві точки: A (-1; 1) і B (1; 0).
Запишемо рівняння прямої і підставимо значення координат цих точок.
y = kx + b - У стандартному вікні рівняння прямої.
Підставами координати точки A:
1 = -k + b
Підставами координати точки B:
0 = k + b
Отримуємо систему рівнянь:
1 = -k + b
0 = k + b
Складемо рівняння:
1 + 0 = -k + b + k + b
1 = 2b
b = 0,5
Підставами в уже готове рівняння 0 = k + b знайдене b:
0 = k + 0,5
k = -0,5
Тепер підставимо відомі k і b в рівняння прямої:
y = -0,5x + 0,5 - Відповідь
Без підставим неяк. Можна кращу відповідь?
Сначала определим значение а из второго уравнения, для чего подставим в него заданные корни (5;-3):
a * x + 3 * y = 11;
a * 5 + 3 * ( - 3) = 11;
a * 5 - 9 = 11;
а * 5 = 11 + 9;
а * 5 = 20;
а = 20/5;
а = 4.
Теперь можно записать заданную систему в нормальном виде:
1) 5 * x + 2 * y = 12;
2) 4 * х + 3 * у = 11.
Умножим 1) на 3, а 2) на 2:
1_1) 15 * x + 6 * y = 36;
2_1) 8 * х + 6 * у = 22.
Теперь вычтем из 1_1) уравнение 2_1):
15 * x + 6 * y - 8 * х - 6 * у = 36 - 22;
15 * x - 8 * х + 6 * y - 6 * у = 36 - 22;
7 * х = 14;
х = 14/7;
х = 2.
Выразим у из 1):
5 * x + 2 * y = 12;
2 * y = 12 - 5 * x;
у = 6 - 2,5 * х.
Подставим х = 2:
у = 6 - 2,5 * 2 = 1.
ответ: (2; 1).
Объяснение:
Сначала определим значение а из второго уравнения, для чего подставим в него заданные корни (5;-3):
a * x + 3 * y = 11;
a * 5 + 3 * ( - 3) = 11;
a * 5 - 9 = 11;
а * 5 = 11 + 9;
а * 5 = 20;
а = 20/5;
а = 4.
Теперь можно записать заданную систему в нормальном виде:
1) 5 * x + 2 * y = 12;
2) 4 * х + 3 * у = 11.
Умножим 1) на 3, а 2) на 2:
1_1) 15 * x + 6 * y = 36;
2_1) 8 * х + 6 * у = 22.
Теперь вычтем из 1_1) уравнение 2_1):
15 * x + 6 * y - 8 * х - 6 * у = 36 - 22;
15 * x - 8 * х + 6 * y - 6 * у = 36 - 22;
7 * х = 14;
х = 14/7;
х = 2.
Выразим у из 1):
5 * x + 2 * y = 12;
2 * y = 12 - 5 * x;
у = 6 - 2,5 * х.
Подставим х = 2:
у = 6 - 2,5 * 2 = 1.
ответ: (2; 1).