Объяснение:
Функция задана формулой y=6x-10 определите
а) чему равно значение y при x=3
б) при каком значение x значений y равно 8
в) проходит ли график функции через точку A (-5;29)
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
у = -6х-10
Таблица:
х -1 0 1
у -16 -10 -4
1)Чтобы найти значение у, нужно известное значение х подставить в уравнение и вычислить у:
х=3
у= 6*3-10=8 у=8 при х=3
2)Чтобы найти значение х, нужно известное значение у подставить в уравнение и вычислить х:
у=8
8=6х-10
-6х= -10-8
-6х= -18
х=3 у=8 при х=3
3)Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение, если левая часть будет равна правой, значит, точка принадлежит графику и наоборот.
А(- 5; 29)
у = 6х-10
29= 6*(-5)-10
29= -30-10
29≠ -40, не проходит.
Объяснение:
йоу,чувак
Мы можем сложить эти два уравнения и получить вместо закорючек:косинусов и синусов - единицу.
Ведь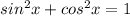 
Т.е при сложении этих уравнений мы получим третье уравнение(да,мы просто сложим друг с другом почленно эти выражения, левая сторона с левой и правая сторона с правой).
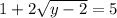
Упс... чуть не забыл ОДЗ! Ведь нельзя забывать,что под корнем у нас могут находиться лишь неотрицательные числа(АУФ),но это пока мы не добрались до комплексного пространства,ну да ладно,оно сейчас не нужно. Итак составим неравенство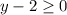 
т.е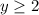 
. Так-с... ОДЗ мы нашли. Вернёмся к истокам.
уравнение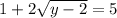 
с одной переменной решается легко,всего-лишь щелчк... возведением в квадрат обеих частей уравнения!
Мы нашли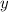 
. И чему он равен? Правильно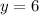 
теперь подставим данное значение 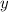в эти уравнения.
И получим следующее
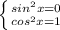
И всё!! Задача почти решена!
Предлагаю тебе обратиться к таблице синусов и косинусов и посмотреть, при каких значениях 
синус обращается в нуль,а косинус в 1.
Удачи тебе, my dear!
1)х∈(-∞, -1), решение системы неравенств.
2)х∈ (-8, 9), решение системы неравенств.
3)х∈(-0,25, 1], решение системы неравенств.
Объяснение:
1) Решить систему неравенств:
−x+4>0
5x<−5
-х> -4
x< -1
x<4 знак меняется х∈(-∞, 4) интервал решений
x< -1 х∈(-∞, -1) интервал решений
Неравенства строгие, скобки круглые.
Отмечаем на числовой оси оба интервала и ищем пересечение решений, то есть, такое решение, которое подходит двум данным неравенствам.
Пересечение х∈(-∞, -1), это и есть решение системы неравенств.
2) Реши систему неравенств:
x²−81<0
x+8>0
Приравняем первое неравенство к нулю и решим квадратное уравнение:
x²−81=0
x²=81
х₁,₂=±√81
х₁= -9
х₂=9
Начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -9 и х=9. По графику ясно видно, что у<0 при х от -9 до 9, то есть, решения неравенства в интервале
х∈ (-9, 9), это решение первого неравенства.
Неравенство строгое, скобки круглые.
Теперь решим второе неравенство:
x+8>0
x> -8
х∈ (-8, +∞), это решение второго неравенства.
Неравенство строгое, скобки круглые.
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Пересечение х∈ (-8, 9), это и есть решение системы неравенств.
3) Реши систему неравенств:
-x>x−2(5x+1)
8−x≥(1+3x)²−9x² в правой части разность квадратов, раскрыть по формуле:
-х>x-10x-2
8-x>=(1+3x-3x)(1+3x+3x)
-x> -9x-2
8-x>=1*(1+6x)
-x+9x> -2
8-x>=1+6x
8x> -2
-x-6x>=1-8
x> -2/8
-7x>= -7
x> -0,25 х∈(-0,25, +∞), это решение первого неравенства.
Неравенство строгое, скобки круглые.
x<=1 х∈(-∞, 1], это решение второго неравенства.
Неравенство нестрогое, х=1 входит в число решений, скобка квадратная. У знаков бесконечности скобка всегда круглая.
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Пересечение х∈(-0,25, 1], это и есть решение системы неравенств.