√(-5x^2+9x+18)/((x+1)∗(7-x) )
(-5x^2+9x+18)/((x+1)∗(7-x) ) ≥ 0
Одз: (x+1)∗(7-x) ≠ 0,
х ≠ -1, х ≠ 7
решим -5x^2+9x+18 = 0
D=441, x1 = -1,2 ; x2 = 3
отмечаем полученные корни на координатный луч. разобьём на промежутки и найдем знаки на каждом промежутке.
(-∞; -1,2] знак "+", [-1,2; -1) знак "-",
(-1; 3] знак "+", [3; 7) знак "-", (7; -∞) знак "+",
нам нужен промежуток где знак "+",
значит x ϵ промежуткам (-∞; -1,2],(-1; 3], (7; -∞).
ответ: x ϵ промежуткам (-∞; -1,2],(-1; 3], (7; -∞).
Разделим все на dx получим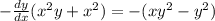 
Сделаем так чтобы в левой части осталось только dy/dx
Получим
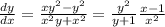
Теперь умножим все на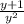 
получаем:
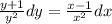
Возьмем интеграл от левой и правой части
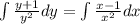
Находим значения интегралов получаем:
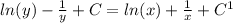Можно объеденить С и С1 в одну константу, назовем ее С.
Этого я думаю достаточно. Чтобы решить задачу Коши нужны начальные условия, к сожалению здесь они не предоставлены. Поэтому попытаемся решить задачу Коши для произвольных начальных условий
y(a)=b , где a,b-константы
найдем сразу ln(y(a))=ln(b) и подставим все в уравнение
получим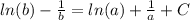
Отсюда
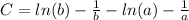
Т.е решеним задачи Коши для произвольных a и b, которые конечно должны принадлежать области определения функций указанных в общем решении уравнения (очевидно, что а и b не равны 0, т.к деление на ноль недопустимо и в общем то говоря а и b>0, если мы конечно не рассматриваем случая когда логарифмическая функция продолжается на комплексное пространство) будет: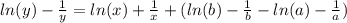
при х<1/2, т.к знаменатель не может быть =0 и подкоренное выражение >0