ответ: cos(γ)=0,925, γ≈22°.
Объяснение:
Пусть АВ=2 см, AC=4 см и BC=5 см. Пусть α, β, γ - углы соответственно при вершинах A, B, C треугольника. Для нахождения косинусов углов используем теорему косинусов:
1. BC²=AB²+AC²-2*AB*AC*cos(α), откуда следует уравнение 25=4+16-2*2*4*cos(α), или 25=20-16*cos(α). Отсюда 16*cos(α)=-5 и cos(α)=-5/16. Тогда α=arccos(-5/16)≈108°.
2. AC²=AB²+BC²-2*AB*BC*cos(β), откуда следует уравнение 16=4+25-2*2*5*cos(β), или 16=29-20*cos(β). Отсюда 20*cos(β)=13 и cos(β)=13/20. Тогда β=arccos(13/20)≈49°.
3. AB²=AC²+BC²-2*AC*BC*cos(γ), откуда следует уравнение 4=16+25-2*4*5*cos(γ), или 4=41-40*cos(γ). Отсюда 40*cos(γ)=37 и cos(γ)=37/40. Тогда γ=arccos(37/40)≈22°
Проверка: сумма углов треугольника должна быть равна 180°. В нашем случае α+β+γ≈108°+49°+22°=179°≈180°, так что углы найдены верно.
Таким образом, наименьшим углом является γ. Его косинус равен 37/40=0,925, а его градусная величина - ≈22°.
Не могу понять ,зачем решать графически ,когда эта интерпретация и есть аналитическое решение ,только в другой форме?
Причём в такой форме ,что не является обоснованным доказательством нашего корня или чего-нибудь другого
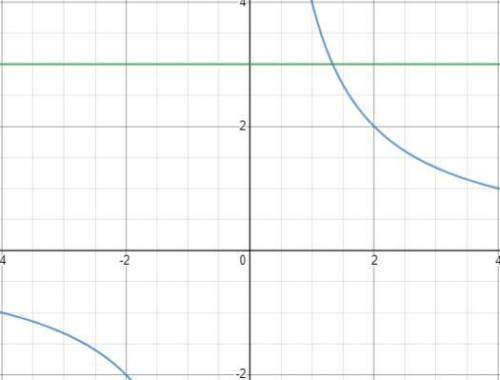
В первом ,да и как во втором уравнении ,у нас справа обратная пропорциональность
Первое уравнение!
Так как ,число а>0 в нашем случаи это 4 ,то функция располагается в первой и третьей четвертях
Так как у нас константа 3 ,то решение будет одно!
Так как просят решить графически ,то ссылаясь на один корень ,то он просто угадывается и это 4/3
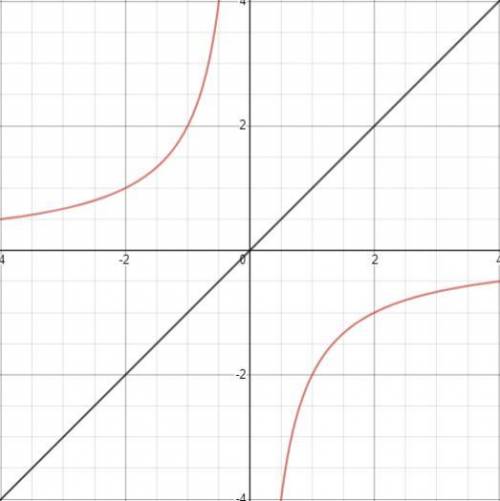
Второе уравнение!
Так как ,число a<0 в нашем случаи это -2,то функция будет располагаться во второй и четвёртой четвертях
Но как можно видеть,слева у нас f(x)=x - прямая
Данная прямая располагается в первой и четвёртых четвертях,так как a>0 ,следовательно данное уравнение не имеет решений!