В решении.
Объяснение:
Решить графически систему уравнений:
у = х² - 7
у = |x|
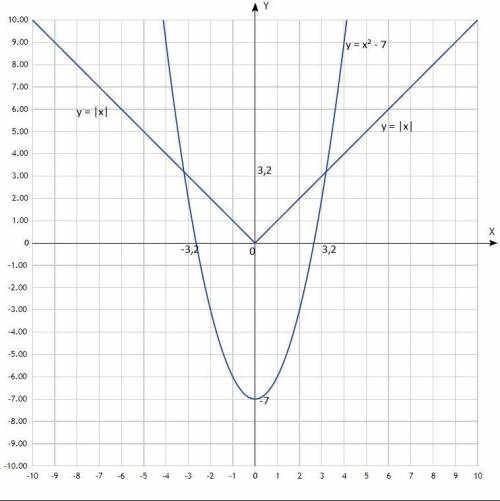
Первый график - парабола со смещённым центром, ветви направлены вверх.
Второй график - график функции модуля (значения у всегда > 0).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х² - 7 у = |x|
Таблицы:
х -4 -3 -2 -1 0 1 2 3 4 х -3 -2 -1 0 1 2 3
у 9 2 -3 -6 -7 -6 -3 2 9 у 3 2 1 0 1 2 3
По вычисленным точкам построить графики.
Согласно графиков, координаты точек пересечения:
(-3,2; 3,2); (3,2; 3,2).
Решения системы уравнений: (-3,2; 3,2); (3,2; 3,2).
В решении.
Объяснение:
Решить графически систему уравнений:
у = х² - 7
у = |x|
Первый график - парабола со смещённым центром, ветви направлены вверх.
Второй график - график функции модуля (значения у всегда > 0).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х² - 7 у = |x|
Таблицы:
х -4 -3 -2 -1 0 1 2 3 4 х -3 -2 -1 0 1 2 3
у 9 2 -3 -6 -7 -6 -3 2 9 у 3 2 1 0 1 2 3
По вычисленным точкам построить графики.
Согласно графиков, координаты точек пересечения:
(-3,2; 3,2); (3,2; 3,2).
Решения системы уравнений: (-3,2; 3,2); (3,2; 3,2).

если я правильно поняла здесь два примера? открываем скобки, преобазуем дроби: x-1целая 15/16+7целых 3/16 = 12целых 10/16. х- 31/16+115/16= 202/16. х+ 84/16= 202/16. неизвестное слева, цифры переносим вправо с другим знаком. х= 202/16 - 84/16. х= 118/16. х= 7 целых 6/16. или сокращенно х= 7 целых 3/8. 15целых 3/28 -(4целых 11/28 +у)=5целых 19/28. открываем скобки: 423/28 - 123/28 - у = 159/28. 300/28 - у= 159/28. переносим "у" с другим знаком 300/28 - 159/28=у. у= 141/28 . или у= 5 целых 1/28.