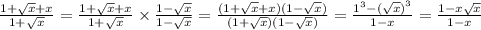
Пояснение:
Выражения такого типа, когда в знаменателе сумма или разность числа и числа под корнем, избавляются от иррациональности простым методом. Вспоминаем формулу сокращенного умножения, разность квадратов:
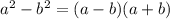 . В нашем примере в знаменателе сумма, то есть
. В нашем примере в знаменателе сумма, то есть 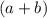 из формулы. Нам нужно найти
из формулы. Нам нужно найти  и умножить на это дробь, чтобы потом получилось
и умножить на это дробь, чтобы потом получилось  , а
, а 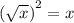 , получится просто число, таким образом избавимся от корня в знаменателе. В нашем случае
, получится просто число, таким образом избавимся от корня в знаменателе. В нашем случае  — это
— это  ,
, 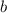 — это
— это 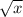 . Соответственно,
. Соответственно,  — это
— это 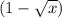 .
.
Важно отметить, что нужно умножить наше выражение не просто на 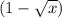 , а на
, а на 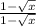 , потому что
, потому что  , а при умножении на 1 значение выражения не измениться. Если умножить просто на
, а при умножении на 1 значение выражения не измениться. Если умножить просто на 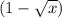 значение выражения поменяется.
значение выражения поменяется.
Вот, собственно, и всё правило.
Ещё, после второго действия, второго =, была использована формула сокращённого умножения — разность кубов:
 . У нас
. У нас 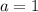 ,
, 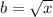 . И получается
. И получается
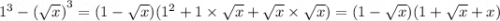 .
.
Объяснение:
1. Чтобы выражение имело смысл, знаменатель не должен быть равен 0 (либо положительный, либо отрицательный). Значит, x - 3  0.
0.
x  3.
3.
ответ: выражение имеет смысл при х 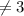 .
.
2.1) 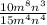 . Сокращаем 10 и 15 на 5, а также вспоминаем, как сокращаются "буквы со степенями":
. Сокращаем 10 и 15 на 5, а также вспоминаем, как сокращаются "буквы со степенями": 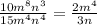
2.2) 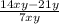 . Здесь нужно заметить, что в числителе дроби за скобку можно вынести 7y:
. Здесь нужно заметить, что в числителе дроби за скобку можно вынести 7y: 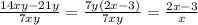
2.3)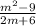 . Важно помнить формулу сокращенного умножения и применить ее в числителе:
. Важно помнить формулу сокращенного умножения и применить ее в числителе: 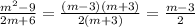
2.4)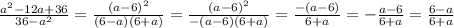 . Здесь в числителе надо наоборот сложить формулу сокращенного умножения, а в знаменателе разложить.
. Здесь в числителе надо наоборот сложить формулу сокращенного умножения, а в знаменателе разложить.
пока что все, а то очень много заданий за )
4
Объяснение:
a<b<0 значит a, b отрицательные числа
a<b, b>a поставим на место а -3,вместо b -2
получиться так -3<-2,
поставим эти цифры на эти утверждения
1) b-a<0 , -2-(-3) =-2+3=1 значит 1<0 = b-a<0 ❌.
2) 2×(-3)=-6 , 2×(-2) =-4 значит -6>-4=2a>2b ❌
3) -(-3)=3 это -а,-(-2) =2 это -b 3<2=-a<-b неправильно❌
4) 1-a>1-b
1-(-3) >1-(-2)
4>3 правильно✔